医療リソース最適化

医療リソース最適化

医療リソース最適化の問題を考え、Pythonで解いてみましょう。

ここでは、病院内のベッドの配分を最適化する問題を例にします。

具体的には、限られた数のベッドを複数の患者グループにどのように配分すれば、全体の患者満足度を最大化できるかを考えます。

問題設定

  • 病院には合計(N)台のベッドがある。
  • 患者グループは(G)グループあり、それぞれのグループには異なる数の患者がいる。
  • 各患者グループ(i)の患者数は(Pi)であり、満足度は(Ui)で与えられる。
  • ベッドの割り当てを最適化して、患者満足度の総和を最大化する。

数理モデル

この問題は整数線形計画問題としてモデル化できます。

変数

  • (xi): 患者グループ(i)に割り当てるベッドの数（整数）

目的関数

最大化する目的関数は全体の満足度の総和です。
maximizeG∑i=1Ui⋅xi

制約条件

  • 各グループに割り当てるベッドの総数は病院のベッド数を超えてはいけません。
    G∑i=1xi≤N
  • 各グループに割り当てるベッドの数は、そのグループの患者数を超えてはいけません。
    0≤xi≤Pi∀i

Python実装

Pythonでこの問題を解くために、数理最適化ライブラリである PuLP を使用します。

まず、必要なライブラリをインストールします。

1
pip install pulp

次に、以下のPythonコードを実行します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import pulp

# パラメータの設定
N = 50  # 病院のベッド数
P = [10, 20, 30, 40]  # 各患者グループの患者数
U = [5, 4, 3, 2]  # 各患者グループの満足度
G = len(P)  # 患者グループの数

# 問題の定義
problem = pulp.LpProblem("Bed_Allocation_Optimization", pulp.LpMaximize)

# 変数の定義
x = [pulp.LpVariable(f"x{i}", lowBound=0, upBound=P[i], cat='Integer') for i in range(G)]

# 目的関数の設定
problem += pulp.lpSum([U[i] * x[i] for i in range(G)]), "Total_Satisfaction"

# 制約条件の設定
problem += pulp.lpSum(x) <= N, "Total_Beds_Constraint"
for i in range(G):
    problem += x[i] <= P[i], f"Patient_Group_{i}_Constraint"

# 問題の解決
problem.solve()

# 結果の表示
print(f"Status: {pulp.LpStatus[problem.status]}")
for i in range(G):
    print(f"Group {i + 1}: Allocate {x[i].varValue} beds")

print(f"Total Satisfaction: {pulp.value(problem.objective)}")

# 結果の可視化
import matplotlib.pyplot as plt

allocated_beds = [x[i].varValue for i in range(G)]
group_labels = [f"Group {i + 1}" for i in range(G)]

plt.bar(group_labels, allocated_beds)
plt.xlabel("Patient Groups")
plt.ylabel("Allocated Beds")
plt.title("Optimal Bed Allocation")
plt.show()

結果の説明

このコードは、病院のベッド配分問題を整数線形計画問題としてモデル化し、最適なベッド配分を求めます。

最後に、各患者グループに割り当てられたベッドの数と、合計の患者満足度を表示し、グラフで可視化します。

[実行結果]

ソースコード解説

1. 必要なライブラリのインポート

1
2
import pulp
import matplotlib.pyplot as plt
  • pulp は線形計画法（LP）を解くためのライブラリです。
  • matplotlib.pyplot はグラフの描画に使用されます。

2. パラメータの設定

1
2
3
4
N = 50  # 病院のベッド数
P = [10, 20, 30, 40]  # 各患者グループの患者数
U = [5, 4, 3, 2]  # 各患者グループの満足度
G = len(P)  # 患者グループの数
  • N は病院の総ベッド数です。
  • P は各患者グループの患者数を表します。
  • U は各患者グループの満足度を表します。
  • G は患者グループの数です。

3. 問題の定義

1
problem = pulp.LpProblem("Bed_Allocation_Optimization", pulp.LpMaximize)
  • ここでは、問題を「Bed_Allocation_Optimization」という名前で定義し、目的が最大化（満足度の合計）であることを指定しています。

4. 変数の定義

1
x = [pulp.LpVariable(f"x{i}", lowBound=0, upBound=P[i], cat='Integer') for i in range(G)]
  • 各患者グループに割り当てるベッド数を表す変数 x[i] を定義します。
  • lowBound=0 は変数の下限を0に設定し、upBound=P[i] は各グループの患者数を上限とします。
  • cat='Integer' は変数が整数であることを指定しています。

5. 目的関数の設定

1
problem += pulp.lpSum([U[i] * x[i] for i in range(G)]), "Total_Satisfaction"
  • 各グループの満足度 U[i] に割り当てるベッド数 x[i] を掛け合わせた総和を目的関数として定義しています。
  • pulp.lpSum はリストの総和を計算します。

6. 制約条件の設定

1
2
3
problem += pulp.lpSum(x) <= N, "Total_Beds_Constraint"
for i in range(G):
    problem += x[i] <= P[i], f"Patient_Group_{i}_Constraint"
  • pulp.lpSum(x) <= N は、全体のベッド数が N 以下であるという制約を設定します。
  • ループ内では、各グループのベッド割り当てがそのグループの患者数を超えないように制約を追加しています。

7. 問題の解決

1
problem.solve()
  • problem.solve() は定義された線形計画問題を解きます。

8. 結果の表示

1
2
3
4
print(f"Status: {pulp.LpStatus[problem.status]}")
for i in range(G):
    print(f"Group {i + 1}: Allocate {x[i].varValue} beds")
print(f"Total Satisfaction: {pulp.value(problem.objective)}")
  • pulp.LpStatus[problem.status] は解のステータス（最適、不可解など）を表示します。
  • ループ内では各グループに割り当てられたベッド数を表示します。
  • pulp.value(problem.objective) は最適な満足度の合計を表示します。

9. 結果の可視化

1
2
3
4
5
6
7
8
allocated_beds = [x[i].varValue for i in range(G)]
group_labels = [f"Group {i + 1}" for i in range(G)]

plt.bar(group_labels, allocated_beds)
plt.xlabel("Patient Groups")
plt.ylabel("Allocated Beds")
plt.title("Optimal Bed Allocation")
plt.show()
  • allocated_beds は各グループに割り当てられたベッド数をリストにします。
  • group_labels は各グループのラベルを作成します。
  • plt.bar は棒グラフを作成します。
  • plt.xlabel, plt.ylabel, plt.title はグラフのラベルとタイトルを設定します。
  • plt.show() はグラフを表示します。

このスクリプトは、病院の限られたベッド数を最も効率的に配分することで患者満足度を最大化するための線形計画問題を解き、その結果を視覚化します。

結果解説

[実行結果]

最適なベッド配分

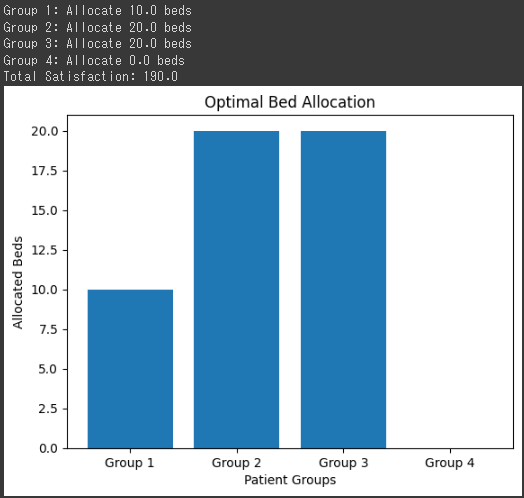
問題を解いた結果、以下のようなベッド配分が最適であることが示されました：

  • Group 1: 10台のベッドを割り当てる
  • Group 2: 20台のベッドを割り当てる
  • Group 3: 20台のベッドを割り当てる
  • Group 4: ベッドを割り当てない

合計の満足度

各グループに割り当てたベッドの数に応じて、全体の満足度の合計は190となります。

詳細な解析

  • Group 1:
    このグループには10人の患者がいて、満足度は5です。
    ベッドを10台割り当てると、満足度は(10×5=50)になります。
  • Group 2:
    このグループには20人の患者がいて、満足度は4です。
    ベッドを20台割り当てると、満足度は(20×4=80)になります。
  • Group 3:
    このグループには30人の患者がいて、満足度は3です。
    ベッドを20台割り当てると、満足度は(20×3=60)になります。
  • Group 4:
    このグループには40人の患者がいて、満足度は2です。
    しかし、このグループにはベッドが割り当てられていないため、満足度は0です。

これらを合計すると、全体の満足度は(50+80+60+0=190)になります。