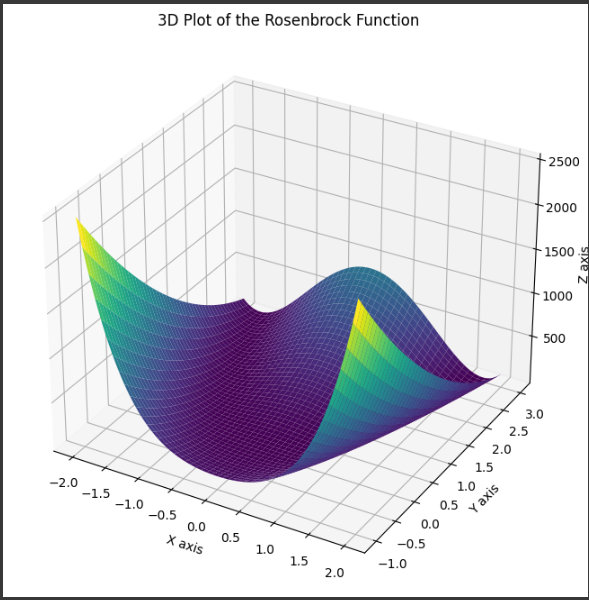
Rosenbrock関数

Rosenbrock関数

Rosenbrock関数は、多変数関数の中でも特に最適化アルゴリズムの性能を評価するために広く使用されるベンチマーク関数の一つです。

この関数は、最小値を求めるための最適化問題において典型的な「谷」の形状を持つため、最適化アルゴリズムのテストに非常に適しています。

Rosenbrock関数の定義

Rosenbrock関数は次のように定義されます：

$$
f(x, y) = (a - x)^2 + b(y - x^2)^2
$$

ここで、$ ( a ) $と$ ( b ) $は定数です。
標準的には$ ( a = 1 ) $と$ ( b = 100 ) $がよく使われます。
この関数は2次元でもっともよく知られていますが、一般的には$ ( n ) $次元にも拡張できます。

主要な特徴

  1. 谷の形状：

    • 関数の形状は、2次元平面上で見ると「谷」のような形をしています。
      これにより、関数の最小値を見つけるのが容易ではなく、アルゴリズムが谷の底に向かって進む必要があります。

  2. 非線形性：

    • 関数は非線形であり、特に$ ( y ) $が$ ( x^2 ) $に依存しているため、複雑な形状を持ちます。
      これにより、局所最小値に陥る可能性が高くなります。

  3. グローバル最小値：

    • 標準的な設定$（( a = 1 ), ( b = 100 )）$では、関数のグローバル最小値は$ ( (x, y) = (1, 1) )$ にあり、この点での関数値は$ ( f(1, 1) = 0 ) $です。

プログラム例

以下のコードは、この関数の3Dグラフを描画するPythonスクリプトです：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Rosenbrock関数の定義
def rosenbrock(x, y, a=1, b=100):
    return (a - x)**2 + b * (y - x**2)**2

# グリッドの作成
x = np.linspace(-2, 2, 400)
y = np.linspace(-1, 3, 400)
X, Y = np.meshgrid(x, y)
Z = rosenbrock(X, Y)

# プロットの設定
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 3Dグラフの描画
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')

# 軸ラベルの設定
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
ax.set_title('3D Plot of the Rosenbrock Function')

# グラフの表示
plt.show()

このコードでは、次の手順を実行しています：

  1. Rosenbrock関数の定義：

    • 関数 rosenbrock(x, y, a, b) を定義し、デフォルトの定数値$ (a=1) $と$ (b=100) $を使用します。

  2. グリッドの作成：

    • $x$軸と$y$軸の範囲を設定し、それに基づいてメッシュグリッド X と Y を作成します。

  3. Rosenbrock関数の計算：

    • メッシュグリッド X と Y に対して関数値 Z を計算します。

  4. プロットの設定：

    • プロットの設定を行い、3Dグラフを描画します。

  5. 3Dグラフの描画：

    • plot_surface を使って、3Dグラフを描画します。
    • カラーマップは viridis を使用し、エッジの色は表示しません。

  6. 軸ラベルとタイトルの設定：

    • 軸ラベルとグラフのタイトルを設定します。

  7. グラフの表示：

    • 最後に plt.show() を使ってグラフを表示します。

この3Dグラフは、Rosenbrock関数の形状を視覚的に示し、関数の複雑さを理解するのに役立ちます。

結果解説

[実行結果]

  • 形状：

    • グラフの形状は、Rosenbrock関数の特性を反映しています。
      特に、グラフは「谷」を形成しており、最小値を中心に広がっています。
      この谷は最適化問題において重要で、最適化アルゴリズムがこの谷の最小値を見つけることを目指します。

  • 最小値：

    • $( a = 1 ) $と$ ( b = 100 ) $の場合、Rosenbrock関数の最小値は$ ( (x, y) = (1, 1) ) $にあります。
      この点では関数値$ ( f(1, 1) = 0 ) $となります。

  • カラーマップ：

    • viridis カラーマップは、関数値の違いを視覚的に強調します。
      高い値は黄色で、低い値は青で表示されます。
      これにより、関数の勾配と極小値が視覚的に識別しやすくなります。

実行結果

このコードを実行すると、Rosenbrock関数の3Dプロットが表示され、関数の複雑な形状を視覚的に確認できます。

これにより、関数の特性と最適化の難しさを理解するのに役立ちます。