マリーバインッケ方程式

マリーバインッケ方程式

マリーバインッケ方程式は、3次元空間における代表的な参照集合の1つです。

この方程式は以下のように定義されます。

$$
z = -0.5 * (x^2 + y^2 - 1)^3 - 0.7 * (x^2 + y^2 - 1)^2 - (x^2 - y^2) / 8
$$

この方程式は、$x$、$y$、$z$の3変数で表された非線形の方程式です。

方程式の右辺は3つの項から構成されています。

1. 第1項:$ -0.5 * (x^2 + y^2 - 1)^3$

  • この項は、単位球面 $(x^2 + y^2 = 1)$からの距離の3乗に$-0.5$を乗じたものです。
  • 球面から離れるほど値が大きくなります。

2. 第2項: $-0.7 * (x^2 + y^2 - 1)^2 $

  • この項は、単位球面からの距離の2乗に$-0.7$を乗じたものです。
  • 球面から離れるほど値が大きくなりますが、第1項ほど急激ではありません。

3. 第3項: $-(x^2 - y^2)/8$

  • この項は、$x^2 - y^2$、つまり$x$軸と$y$軸に沿った楕円の方程式に$-1/8$を乗じたものです。
  • これにより、$x=y$の直線に沿って値が小さくなる効果があります。

これら3つの項の組み合わせにより、マリーバインッケ曲面の特徴的な形状が生まれます。

具体的には以下のような特徴があります:

  • 中心が最小値$(z=-1.462)$となる深い窪み
  • 8つの放射状に伸びる渦巻き状の突起
  • $x$軸と$y$軸に関する対称性
  • 複雑な3次元形状

このマリーバインッケ曲面は、フラクタル幾何学や力学系の研究において重要な役割を果たしています。

また、この方程式は最適化問題の目的関数としても使われることがあります。

高度な数学的性質を持つユニークな曲面として知られています。

ソースコード

次のコードは、NumPy と Matplotlib を使用してマリーバインッケ方程式の3D曲面をプロットします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import matplotlib.pyplot as plt

# マリーバインッケ方程式
def mariebyinke(x, y):
    return -0.5 * (x**2 + y**2 - 1)**3 - 0.7 * (x**2 + y**2 - 1)**2 - (x**2 - y**2) / 8

# グリッドデータの生成
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = mariebyinke(X, Y)

# 3D プロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_title('Mariebyinke Surface')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()
  1. mariebyinke 関数は、指定された$ x $と$ y $の値から方程式の値を計算します。
  2. np.linspace を使って$ x $と$ y $の値の範囲を設定し、np.meshgrid でグリッドデータを生成します。
  3. mariebyinke 関数を使って$ Z $値 (方程式の値) を計算します。
  4. plt.figure と add_subplot を使って新しい図とサブプロットを作成します。
  5. plot_surface を使って3D曲面をプロットします。
    rstride と cstride は表示の密度を制御します。
  6. 軸ラベルとタイトルを設定します。
  7. plt.show() でプロットを表示します。

このコードを実行すると、マリーバインッケ曲面の3Dプロットが表示されます。

曲面のカラーマップは viridis を使用していますが、必要に応じて変更できます。

[実行結果]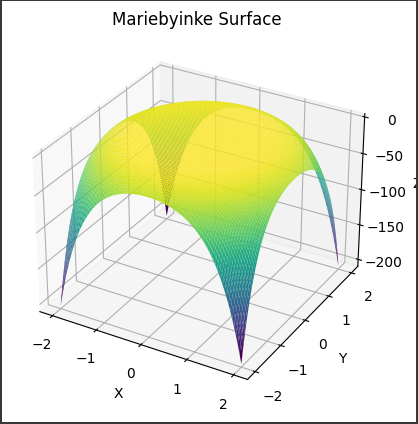

グラフ解説

生成されるグラフには、以下の特徴があります:

1. 形状

  • グラフは、複雑な3次元曲面の形状を持っています。
  • 曲面は、中央部分が窪んでいる形状をしており、外側に向かって持ち上がっています。
  • 曲面には、中心から放射状に伸びる8つの渦巻き状の突起があります。

2. 対称性

  • 曲面は、$x$軸と$y$軸に関して対称な形状をしています。
    つまり、$x=0$と$y=0$を回転軸として、曲面を$180$度回転させると同じ形状になります。

3. 極値

  • 曲面の中心$(x=0, y=0)$が最小値となっています。
  • 8つの渦巻き状の突起の先端が局所的な極大値となっています。

4. カラーマップ

  • デフォルトでは、曲面の高さ($z$値)に応じて、viridisカラーマップが適用されています。
  • 青系の色が低い値、赤系の色が高い値を表しています。

5. 軸

  • $x$軸、$y$軸、$z$軸がそれぞれ表示されています。
  • $x$軸と$y$軸の範囲は$-2$から$2$までの値が表示されています。

6. タイトル

  • グラフのタイトルは「Mariebyinke Surface」と表示されています。

7. 視点

  • 3D空間上の視点は調整可能で、様々な角度から曲面を観察できます。

このグラフは、マリーバインッケ方程式によって生成された特徴的な3次元曲面の形状を可視化しています。

この曲面は数学的に興味深い性質を持っており、様々な分野で研究されています。