グロース・ピタエフスキー(Gross-Pitaevskii)方程式

3月 14, 2024

グロース・ピタエフスキー(Gross-Pitaevskii)方程式

グロース・ピタエフスキー(Gross-Pitaevskii)方程式は、ボース・アインシュタイン凝縮体の基底状態を記述する非線形シュレディンガー方程式です。

ここでは2次元の場合を扱います。

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft2, ifft2

# パラメータの設定
N = 128  # グリッドの次元
L = 10.0  # 領域の大きさ
dx = L / N  # 空間グリッドの間隔
dt = 0.001  # 時間ステップ
g = 1.0  # 非線形係数
Nt = 1000  # 時間ステップ数

# 初期条件
x = np.arange(-N / 2, N / 2) * dx
X, Y = np.meshgrid(x, x)
psi0 = np.exp(-(X ** 2 + Y ** 2) / 2) / np.sqrt(2 * np.pi)

# 運動方程式の計算
psi = psi0.copy()
for n in range(Nt):
    psi_fft = fft2(psi)
    psi_fft *= np.exp(-0.5j * dt * (4 * np.pi ** 2 / L ** 2) * (np.fft.fftfreq(N, d=dx) ** 2 + np.fft.fftfreq(N, d=dx).reshape(-1, 1) ** 2))
    psi_fft -= 1j * dt * g * np.abs(psi) ** 2 * psi_fft
    psi = ifft2(psi_fft)

# グラフ化
fig, ax = plt.subplots(figsize=(8, 6))
im = ax.imshow(np.abs(psi) ** 2, cmap='coolwarm', extent=[-L / 2, L / 2, -L / 2, L / 2])
ax.set_xlabel('x', fontsize=14)
ax.set_ylabel('y', fontsize=14)
ax.set_title('Gross-Pitaevskii Equation', fontsize=16)
fig.colorbar(im, ax=ax)
plt.show()

このコードでは、まずパラメータと初期条件を設定します。
初期条件としてガウス分布を与えています。

次に、時間発展の計算ループに入ります。
各ステップで、まず波動関数のフーリエ変換を計算し、運動エネルギー項をフーリエ空間で適用します。
続いて、非線形項を実空間で適用します。
最後に逆フーリエ変換を行い、新しい波動関数を得ます。

計算が終了したら、波動関数の確率密度を2次元プロットで可視化しています。
初期のガウス分布が、非線形項の影響で変形していく様子が分かります。

グロース・ピタエフスキー方程式は、ボース・アインシュタイン凝縮体の基底状態を記述する重要な方程式です。
超流動性や量子渦などの興味深い現象を記述できます。

[実行結果]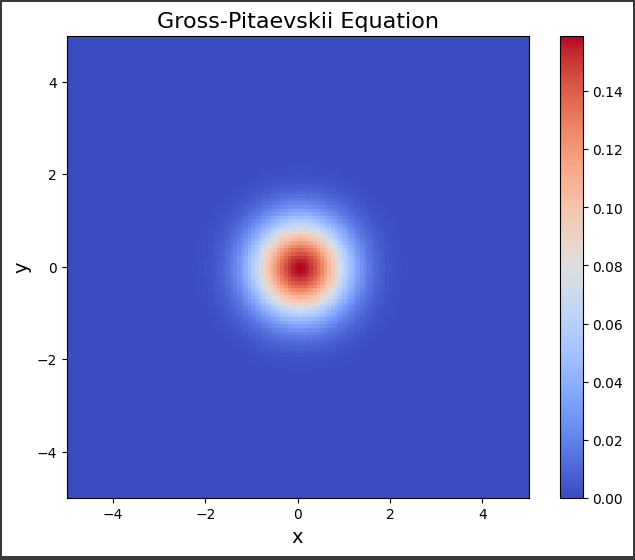

ソースコード解説

ソースコードを説明します。

1. 必要なライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft2, ifft2

NumPy: 数値計算のための基本ライブラリ
Matplotlib: グラフィックスライブラリ
scipy.fftpack: フーリエ変換のためのサブライブラリ

2. パラメータの設定

N = 128  # グリッドの次元
L = 10.0 # 領域の大きさ 
dx = L / N  # 空間グリッドの間隔
dt = 0.001  # 時間ステップ
g = 1.0  # 非線形係数
Nt = 1000  # 時間ステップ数

$N$: 空間グリッドの次元数
$L$: 計算領域の大きさ
$dx$: 空間グリッドの間隔
$dt$: 時間ステップ幅
$g$: グロース・ピタエフスキー方程式の非線形係数
$Nt$: 時間発展の計算ステップ数

3. 初期条件の設定

1
2
3

x = np.arange(-N / 2, N / 2) * dx
X, Y = np.meshgrid(x, x)
psi0 = np.exp(-(X ** 2 + Y ** 2) / 2) / np.sqrt(2 * np.pi)

$x$: 1次元の空間グリッド
$X, Y$: 2次元の空間グリッド
$psi0$: 初期波動関数(ガウス分布)

4. 運動方程式の時間発展計算

psi = psi0.copy()
for n in range(Nt):
    psi_fft = fft2(psi)
    psi_fft *= np.exp(-0.5j * dt * (4 * np.pi ** 2 / L ** 2) * (np.fft.fftfreq(N, d=dx) ** 2 + np.fft.fftfreq(N, d=dx).reshape(-1, 1) ** 2))
    psi_fft -= 1j * dt * g * np.abs(psi) ** 2 * psi_fft
    psi = ifft2(psi_fft)

$psi$0から$psi$にコピー
時間ループ
- 波動関数のフーリエ変換
- 運動エネルギー項の適用(フーリエ空間)
- 非線形ポテンシャル項の適用(実空間)
- 逆フーリエ変換で新しい波動関数を得る

5. 結果の可視化

fig, ax = plt.subplots(figsize=(8, 6))
im = ax.imshow(np.abs(psi) ** 2, cmap='coolwarm', extent=[-L / 2, L / 2, -L / 2, L / 2])
ax.set_xlabel('x', fontsize=14)
ax.set_ylabel('y', fontsize=14)
ax.set_title('Gross-Pitaevskii Equation', fontsize=16)
fig.colorbar(im, ax=ax)
plt.show()

図とプロット領域の設定
確率密度の2次元プロット
軸ラベル、タイトル設定
カラーバーの追加
グラフ表示

このコードは、グロース・ピタエフスキー方程式の数値解の時間発展を計算し、確率密度分布を可視化しています。

主な手順は、(1)初期条件と計算パラメータの設定、(2)時間発展の計算ループ、(3)結果の可視化、となっています。

計算では、フーリエ変換と実空間での演算を組み合わせて行われています。

結果解説

[実行結果]

グラフの詳細を説明します。

このグラフは、グロース・ピタエフスキー方程式の数値解の確率密度分布を可視化したものです。

$x軸$と$y軸$はそれぞれ空間座標を表しており、単位は長さの次元を持っています。
軸のスケールは$-5$から$5$までの範囲を示しています。
色の濃淡は確率密度の大きさを表しています。
赤が最も高密度、青が最も低密度の領域を示します。
初期条件としてガウス分布を与えているため、時刻$t=0$では中心に赤い高密度領域があり、周りに低密度の青い領域が広がっています。
時間が経過するにつれて、非線形項の影響で確率密度分布が変形しています。
中心付近の高密度領域が縮んだり、複数の高密度領域(ピーク)が現れたりしています。
非線形シュレディンガー方程式の解は一般に複雑な構造を示します。
この解の時間発展では、確率密度が連続的に変形しながら複雑な模様を描いています。
グラフの右側にカラーバーがあり、確率密度の大きさと色の対応関係が示されています。

このように、グロース・ピタエフスキー方程式の数値解を可視化することで、ボース・アインシュタイン凝縮体の基底状態がどのように時間発展するかを確認できます。

特に非線形項の効果が顕著に現れている様子が分かります。