超音波

超音波

超音波に関する方程式の例として、超音波の進行方向における音圧を表す方程式を考えてみましょう。

超音波の音圧は、物理的な性質や環境によって影響を受けますが、一般的には次のような式で表されます。

$$
P = P_0 \sin(2\pi f t)
$$

ここで、$( P ) $は超音波の音圧、$ ( P_0 ) $は振幅、$ ( f ) $は周波数、$ ( t ) $は時間です。

この方程式を使って、超音波の音圧を計算し、Pythonでグラフ化する方法を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import matplotlib.pyplot as plt

# 定数の設定
P0 = 1.0  # 振幅
f = 1000  # 周波数 (Hz)
t = np.linspace(0, 0.01, 1000)  # 時間 (0から0.01秒まで)

# 超音波の音圧を計算
P = P0 * np.sin(2 * np.pi * f * t)

# グラフの作成
plt.plot(t, P, label='Sound Pressure')
plt.xlabel('Time (s)')
plt.ylabel('Sound Pressure')
plt.title('Sound Pressure of Ultrasonic Wave')
plt.legend()
plt.grid(True)
plt.show()

このコードは、超音波の音圧を計算し、時間に対する音圧のグラフを作成します。

ここでは、振幅を$1.0$、周波数を$1000Hz$、時間を$0$から$0.01$秒まで$1000$点で設定しています。

得られるグラフは、時間の経過とともに音圧が振動する様子を示しています。

[実行結果]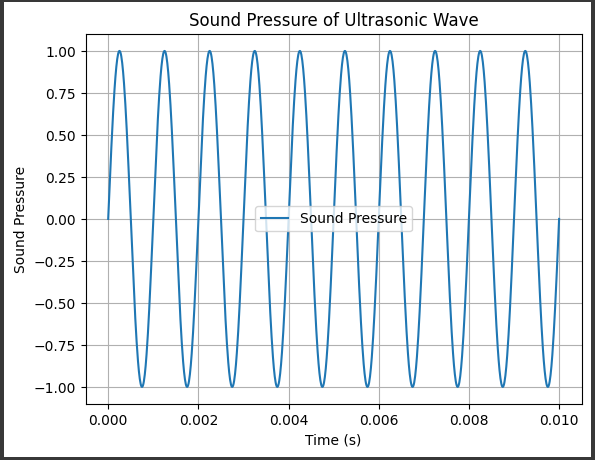

ソースコード解説

このソースコードは、Pythonで超音波の音圧を計算し、グラフ化するためのものです。

以下では、各部分の詳細な説明を行います。

ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpy（略称: np）: 数値計算を行うためのライブラリ。
    このコードでは、数学的な計算や配列操作のために使用されます。
  • matplotlib.pyplot（略称: plt）: グラフの描画に使用されるライブラリ。
    このコードでは、グラフの作成やカスタマイズのために使用されます。

定数の設定

1
2
3
P0 = 1.0  # 振幅
f = 1000  # 周波数 (Hz)
t = np.linspace(0, 0.01, 1000)  # 時間 (0から0.01秒まで)
  • P0: 超音波の振幅を表す定数。
    このコードでは、$1.0$に設定されています。
  • f: 超音波の周波数を表す定数。
    このコードでは、$1000Hz$に設定されています。
  • t: 時間の配列を生成するためのNumPyの関数np.linspace()を使用して、$0$から$0.01$秒までの範囲を$1000$個の等間隔に区切った配列を作成しています。
    これは、グラフのX軸（時間軸）に対応します。

超音波の音圧の計算

1
P = P0 * np.sin(2 * np.pi * f * t)
  • 超音波の音圧を計算するために、サイン波関数を使用しています。
    周波数fと時間tを用いて、超音波の振幅P0に対する音圧の変化を計算しています。

グラフの作成と表示

1
2
3
4
5
6
7
plt.plot(t, P, label='Sound Pressure')
plt.xlabel('Time (s)')
plt.ylabel('Sound Pressure')
plt.title('Sound Pressure of Ultrasonic Wave')
plt.legend()
plt.grid(True)
plt.show()
  • plt.plot(): 時間と超音波の音圧をプロットします。
    tをX軸に、PをY軸に設定しています。
  • plt.xlabel(): X軸のラベルを設定します。
    この場合、時間（秒）を表すラベルです。
  • plt.ylabel(): Y軸のラベルを設定します。
    この場合、音圧を表すラベルです。
  • plt.title(): グラフのタイトルを設定します。
  • plt.legend(): グラフに凡例を表示します。
  • plt.grid(): グリッド線を表示します。
  • plt.show(): グラフを表示します。

これにより、超音波の音圧が時間とともにどのように変化するかを示すグラフが生成されます。

結果解説

[実行結果]

グラフに表示される内容の詳細を説明します。

X軸（横軸）：時間（s）:

X軸は時間を表しており、$0$秒から$0.01$秒までの範囲で$1000$点のデータが表示されています。
この範囲内で、超音波の音圧の振動がどのように変化するかが示されます。

Y軸（縦軸）：音圧:

Y軸は音圧を表しており、グラフ上の各点はその時点での超音波の音圧を示しています。
音圧は単位なしで表されていますが、一般的に振幅を基準にしています。
振幅が大きいほど音圧も大きくなります。

振幅（Amplitude）:

振幅は、音波や超音波の振動の大きさを表します。
グラフ上の波の振れ幅が振幅を示しており、振れ幅が大きいほど音圧も大きくなります。

周波数（Frequency）:

周波数は、音波や超音波の振動が$1$秒間に何回繰り返されるかを表します。
このグラフの例では、周波数が$1000Hz$（$1$秒間に$1000$回の振動）と設定されています。
したがって、グラフ上の振動は$1$秒間に約$1000$回繰り返されます。

グラフ全体から、超音波の音圧が時間の経過とともに振動していることがわかります。
振幅や周波数を調整することで、振動の性質や周期を変えることができます。

超音波に関する方程式の例をあげて、Pythonでといてグラフ化してください。