虚数 3Dグラフ化

虚数は、実数部と虚数部から構成される数学の概念で、虚数単位 (i)は(√−1)と表現されます。

複素数は通常(a+bi)の形で表され、(a)が実数部、(b)が虚数部です。

虚数は様々な科学や工学の分野で利用され、波動解析や制御理論、量子力学などで重要な役割を果たします。

以下に、[f(z)=sin(z)+cos(2z)+e0.5z=0]という方程式の3DグラフをPythonで描画します。

この例は虚数を含む関数を視覚的に理解するのに役立つものです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 方程式の例: f(z) = sin(z) + cos(2z) + e^(0.5z)
def complex_equation(z):
    return np.sin(z) + np.cos(2*z) + np.exp(0.5*z)

# 複素数を生成
real_part = np.linspace(-4, 4, 400)
imaginary_part = np.linspace(-4, 4, 400)
real, imag = np.meshgrid(real_part, imaginary_part)
z = real + 1j * imag

# 方程式の値を計算
result = complex_equation(z)

# 3Dグラフ化
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(real, imag, np.abs(result), cmap='viridis', alpha=0.8)

ax.set_title('Complex Equation: $f(z) = \sin(z) + \cos(2z) + e^{0.5z} = 0$')
ax.set_xlabel('Real Part')
ax.set_ylabel('Imaginary Part')
ax.set_zlabel('|f(z)|')
plt.show()

この例では、虚数を含む関数の3Dプロットを通じて、虚数部の変化が方程式に与える影響を視覚化しています。

[実行結果]

ソースコード解説

以下に、ソースコードの各部分の説明を示します。

1. 必要なライブラリのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • numpy: 数学的な計算を行うための便利なツールを提供するライブラリ。
  • matplotlib.pyplot: グラフの描画に使用されるライブラリ。
  • mpl_toolkits.mplot3d.Axes3D: 3Dグラフを描画するための追加のツールキット。

2. 複雑な方程式の定義:

1
2
def complex_equation(z):
    return np.sin(z) + np.cos(2*z) + np.exp(0.5*z)
  • complex_equation:(f(z)=sin(z)+cos(2z)+e0.5z)という複雑な方程式を計算する関数。

3. 複素数の生成:

1
2
3
4
real_part = np.linspace(-4, 4, 400)
imaginary_part = np.linspace(-4, 4, 400)
real, imag = np.meshgrid(real_part, imaginary_part)
z = real + 1j * imag
  • np.linspace(): 指定された範囲で等間隔の数値を生成。
  • np.meshgrid(): 2Dグリッド座標の生成。
  • z: 生成された複素数。

4. 方程式の値の計算:

1
result = complex_equation(z)
  • result: 生成された複素数に対して方程式を計算し、その結果を格納。

5. 3Dグラフの作成:

1
2
3
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(real, imag, np.abs(result), cmap='viridis', alpha=0.8)
  • plt.figure(): 新しい図を作成。
  • fig.add_subplot(): サブプロットを追加。
  • ax.plot_surface(): 3Dサーフェスプロットを描画。
  • cmap='viridis': カラーマップを ‘viridis’ に設定。
  • alpha=0.8: 透明度を設定。

6. グラフのラベルと表示:

1
2
3
4
5
ax.set_title('Complex Equation: $f(z) = \sin(z) + \cos(2z) + e^{0.5z} = 0$')
ax.set_xlabel('Real Part')
ax.set_ylabel('Imaginary Part')
ax.set_zlabel('|f(z)|')
plt.show()
  • グラフにタイトルと軸ラベルを追加。
  • plt.show(): グラフを表示。

このコードは、複雑な方程式の複素平面上での振る舞いを3Dグラフで可視化する例です。

結果解説

[実行結果]

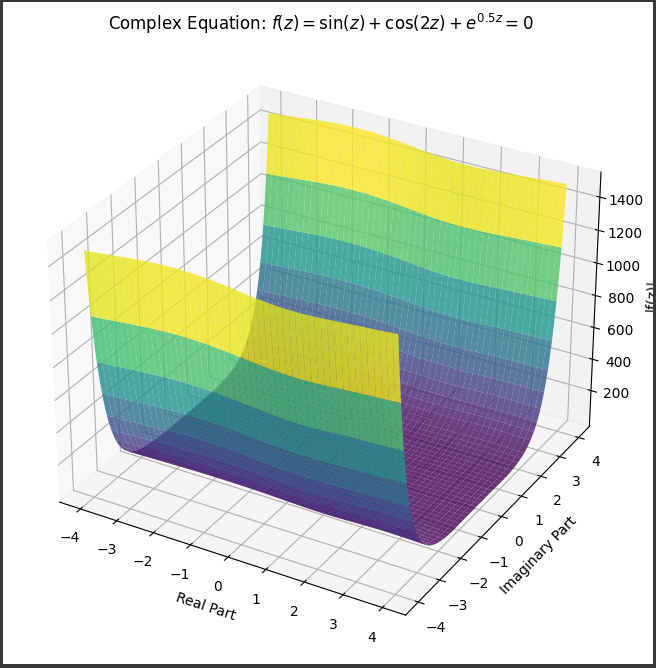
上記の3Dグラフは、[f(z)=sin(z)+cos(2z)+e0.5z]という方程式の絶対値を視覚化しています。

この方程式は虚数(z)を含んでおり、その絶対値（モジュラス）を求めています。

  • x軸は実数部を、y軸は虚数部を表しています。
    z軸は方程式の絶対値 (|f(z)|)を示しています。
  • グラフ上の点は、複素平面上の異なる(z)の値に対応しています。
  • グラフの色は、絶対値の大小を示しており、色が濃いほど絶対値が大きいことを表しています。

このグラフは、複素数(z)を方程式に代入したときの絶対値の変化を表しています。

虚数部の変化が方程式に与える影響を理解するのに役立ちます。

グラフを観察することで、特定の領域で方程式がどのように振る舞うかを視覚的に捉えることができます。