クーロンの法則 3Dグラフ

1月 12, 2024

クーロンの法則 3Dグラフ

物理学の中でも電磁気学に現れるポテンシャル方程式であるクーロンの法則を題材に、Pythonで3Dグラフ化してみましょう。

クーロンの法則によれば、2つの電荷間の力は各電荷の大きさと距離の二乗に反比例します。

ここでは負電荷の周りの電位分布を3Dで可視化してみましょう。

必要なライブラリをインポートしましょう：

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

次に、電位計算と可視化関数をそれぞれ定義します：

def potential(x, y, q, pos):
    k = 8.99e9
    return k*q/np.sqrt((x-pos[0])**2 + (y-pos[1])**2)

def plot_potential(q, pos):
    x = np.linspace(-10, 10, 100)
    y = np.linspace(-10, 10, 100)
    x, y = np.meshgrid(x, y)
    z = potential(x, y, q, pos)

    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    ax.plot_surface(x, y, z, cmap='jet')
    plt.show()

そして、電荷 $-q$が$-1$、位置が$(0, 0)$の場合の電位をプロットします：

1	plot_potential(-1, [0, 0])

それぞれの関数で、potentialでは電荷 $q$の大きさと位置から電位を計算し、plot_potentialではその電位を3Dグラフでプロットしています。

電荷の位置は$0,0$とし、$x$と$y$の範囲を$-10$から$10$までとしています。

また、電位の計算にはクーロンの定数 $k$を用いています。

[実行結果]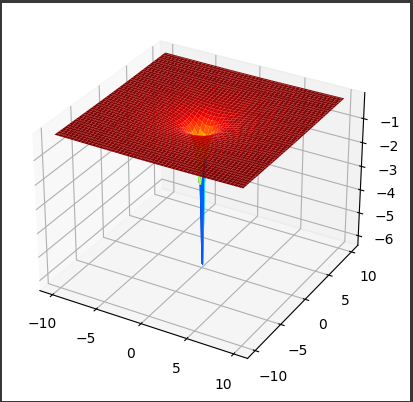

ソースコード解説

このソースコードは、電荷が生じる空間における電位を3Dプロットするためのものです。

以下に、ソースコードの章立てと説明を示します。

1. 必要なライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

NumPy: 数学的な演算を効率的に行うためのライブラリ。
Matplotlib: グラフ描画のためのライブラリ。
mpl_toolkits.mplot3d: 3Dプロットを生成するためのツールキット。

2. 電位を計算する関数 `potential` の定義

1
2
3

def potential(x, y, q, pos):
   k = 8.99e9
   return k*q/np.sqrt((x-pos[0])**2 + (y-pos[1])**2)

potential 関数は、与えられた座標 (x, y) における電位を計算します。
q: 電荷の大きさ。
pos: 電荷の位置。

3. 電位を3Dプロットする関数 `plot_potential` の定義

def plot_potential(q, pos):
   x = np.linspace(-10, 10, 100)
   y = np.linspace(-10, 10, 100)
   x, y = np.meshgrid(x, y)
   z = potential(x, y, q, pos)

   fig = plt.figure()
   ax = fig.add_subplot(111, projection='3d')
   ax.plot_surface(x, y, z, cmap='jet')
   plt.show()

plot_potential 関数は、指定された電荷 (q) と位置 (pos) に基づいて、空間内の電位を3Dサーフェスプロットとして描画します。
x と y は座標軸の範囲を表し、これらの座標で x, y 平面上の格子点を生成します。
potential 関数を使用して各格子点で電位を計算し、それを3Dサーフェスプロットとして描画します。

4. 関数の呼び出し

1	plot_potential(-1, [0, 0])

-1 の電荷が原点 [0, 0] にある場合の電位をプロットします。

このコードは、電場のポテンシャルの視覚化を行います。

結果解説

[実行結果]

このグラフは、電荷が生じる空間における電位を表しています。

具体的には、電荷が原点 (0, 0) にあり、その電荷が周囲の空間に生じる電位を3Dサーフェスプロットで視覚化しています。

以下はグラフの詳細な説明です：

1. 座標軸と目盛り：

X軸とY軸はそれぞれ -10 から 10 の範囲で、2次元平面を表します。
Z軸は電位を表し、色で表示されています。

2. サーフェスプロット：

3Dサーフェスプロットは、座標平面上の各点における電位を表しています。
カラーマップ “jet” が使用されており、色の濃淡が電位の変動を示しています。

3. 電荷の位置と影響範囲：

電荷は原点$ (0, 0) $にあります。
この点から離れるほど電位が変動します。
グラフ上で、原点の周りに盛り上がりやくぼみが見られ、これが電荷による電位の影響を示しています。

4. 濃淡と電位の関係：

カラーマップにより、電位が濃い色ほど高いことを示しています。
つまり、電位が高い領域ではより濃い色調が見られます。

このグラフは、電荷が空間に与える電位の変動を見ることができるものであり、電場の概念を直感的に理解するのに役立ちます。