モジュロ関数

モジュロ関数

複雑な数式の例として、複素数のモジュロ関数を考えてみましょう。

この関数は、複素数 $z$に対して、$z$の絶対値（モジュロ）を計算します。

複素数$z$は、実部（x座標）と虚部（y座標）から成り立ちます。

以下に、この数式をPythonでグラフ化するコードを示します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt

# 複素数zの範囲を設定
N = 500
lim = 4

# 複素数zの実部と虚部のグリッドを生成
x, y = np.meshgrid(np.linspace(-lim, lim, N), np.linspace(-lim, lim, N))
z = x + 1j*y

# 複素数zのモジュロを計算
f = abs(1/(z**2-4))
f[f > 1.3] = 1.3 # 極（無限大）の近くで関数を切る

# 3Dプロットの設定
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(x, y, f, cmap="viridis", shade=True, alpha=1)
ax.set_xlabel("Re(z)", size=14)
ax.set_ylabel("Im(z)", size=14)
ax.set_title("|f(z)| = |1/(z^2-4)|", size=18, pad=30)

plt.show()

このコードでは、numpyのmeshgrid関数を使用して複素数 $z$の実部と虚部のグリッドを生成し、それを使用して複素数 $z$を計算しています。

そして、複素数 $z$のモジュロを計算し、それを3Dプロットに使用しています。

[実行結果]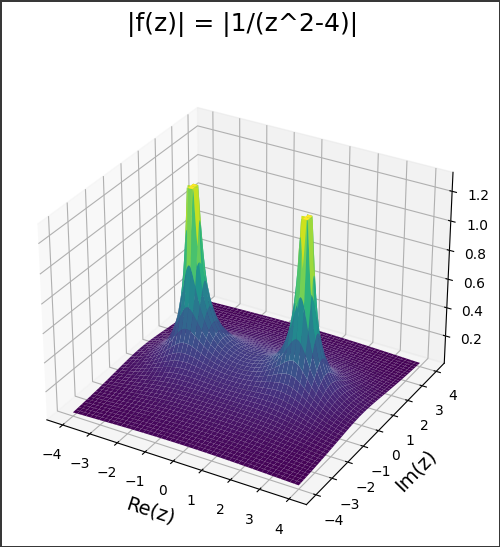

ソースコード解説

ソースコードを解説します。

1. 必要なライブラリのインポート:

numpy と matplotlib を使用します。
numpy は数値計算を行うために使用され、matplotlib はグラフのプロットに使用されます。

2. 複素数zの範囲の設定:

  • N = 500: グリッドの数を定義します。
  • lim = 4: 複素平面の範囲を設定します。
    実部と虚部の両方が$ -4 $から$ 4 $の範囲で設定されます。

3. 複素数zの実部と虚部のグリッドを生成:

  • np.meshgrid() を使って、$ -4 $から$ 4 $までの実部と虚部の範囲でグリッドを生成します。

4. 複素数zのモジュロ計算:

  • $ ( f(z) = \left| \frac{1}NaN \right| ) $の計算を行います。
    ここでは abs() を使用して、モジュロ（絶対値）を求めます。
  • 極（無限大）の近くで値が非常に大きくなるのを防ぐために、一定の値（ここでは$1.3$）を超える部分を$1.3$にクリッピングしています。

5. 3Dプロットの設定:

  • plt.figure() で図を作成し、projection="3d" を指定して3Dプロットを作成します。
  • ax.plot_surface() で複素関数の3Dプロットを作成します。
    カラーマップは “viridis” を使っています。
  • ax.set_xlabel()、ax.set_ylabel()、ax.set_title() でそれぞれx軸、y軸、タイトルのラベルを設定しています。

6. グラフの表示:

  • plt.show() でグラフを表示します。

このコードは、複素関数の特定の領域におけるモジュロの振る舞いを可視化するものです。

結果解説

[実行結果]

上記のPythonコードで生成される3Dグラフは、複素数$z$のモジュロを計算した結果を表示しています。
ここで$z$は複素数で、実部（x座標）と虚部（y座標）から成り立ちます。

具体的には、x軸とy軸は複素数$z$の実部と虚部を表し、z軸は複素数$z$のモジュロを表しています。
つまり、3Dグラフの一つの点は、複素数$z$ （実部と虚部のペア）とそのモジュロを表しています。

また、このグラフは$ |1/(z^2-4)| $の形をしています。

これは、複素数$z$の二乗から4を引いたものの逆数の絶対値を計算したものです。

この関数は、$ z^2-4 $が$0$に等しいとき（つまり、$z$が$±√4=±2のとき）$には無限大となります。

そのため、このグラフでは、$z$が$±2$の近くで関数値が$1.3$に切られています。