複素数関数 3Dグラフ化

複素数関数 3Dグラフ化

複素数関数の方程式では、複素数平面上の方程式の解の振る舞いを視覚化できます。

以下は、方程式の解をプロットする例です。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# グリッドを作成
real = np.linspace(-5, 5, 100)
imag = np.linspace(-5, 5, 100)
real, imag = np.meshgrid(real, imag)
z = real + 1j * imag

# 方程式
eqn = z**3 - 1  # 方程式の例

# 3Dグラフの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(np.real(z), np.imag(z), np.real(eqn), c=np.real(eqn), cmap='viridis')

# グラフのラベル設定
ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')
ax.set_zlabel('Real part of the equation')
ax.set_title('Graph of a complex equation')

plt.show()

この例では、$ (z^3 - 1) $という複素数の3次方程式を使用しています。

これは複素数平面上の方程式です。

3Dプロットは、実部と虚部の関係を示し、方程式の解の振る舞いを可視化します。

[実行結果]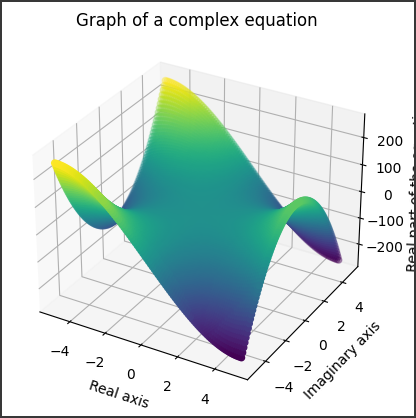

ソースコード解説

このコードは、複素平面上で$ (z^3 - 1) $のグラフを3Dで描画しています。

ここでの$ (z) $は、複素数$ (z = x + yi) $で表され、実部が$ (x) $軸、虚部が$ (y) $軸にマッピングされています。

1. グリッドの作成:

np.linspace を用いて、実数と虚数の範囲を指定し、それぞれ$ (x) $軸および$ (y) $軸の値を生成し、meshgrid を使って複素平面上の格子点を作成しています。

2. 方程式の定義:

z**3 - 1 という方程式を定義し、eqn に格納しています。これは$ (z^3 - 1 = 0) $という方程式を表しています。

3. 3Dグラフの描画:

matplotlib を用いて、3Dの散布図を描画しています。
scatter 関数を使い、複素数$ (z) $の実部と虚部に対応する点をプロットし、色は$ (z^3 - 1) $の実部によって変わります。

4. 軸ラベルとタイトルの設定:

set_xlabel、set_ylabel、set_zlabel を用いてそれぞれ$ (x) $軸、$ (y) $軸、$ (z) $軸のラベルを設定し、set_title でグラフのタイトルを設定しています。

5. グラフの表示:

plt.show() を使って、作成した3Dグラフを表示しています。

このグラフは、複素平面上で$ (z^3 - 1) $の方程式を表し、その実部がゼロになる$ (z) $の値を表しています。

それにより得られる図形は、3次元曲線になります。

結果解説

[実行結果]

このグラフは、複素平面上で方程式$ ( z^3 - 1 ) $を表現しています。

グラフは複素数 $ ( z = x + yi ) $の実部、虚部、および方程式 $ ( z^3 - 1 ) $の実部を3Dで表現しています。

具体的には、複素平面内で実部が$ ( x ) $軸、虚部が$ ( y ) $軸、そして$ ( z^3 - 1 ) $の実部が$ ( z ) $軸にマッピングされています。

グラフ上の点は複素数 $ ( z ) $の実部と虚部に基づいて配置され、色は$ ( z^3 - 1 ) $の実部を示しています。

このグラフは$ ( z^3 - 1 ) $の実部が$ ( 0 ) $になるような$ ( z ) $の値を示しており、その結果得られる図形は特定の形を持つ3次元曲線です。

この方程式が複素平面上でどのように振る舞うかを示しています。