ヴァンデル・ポルト方程式

ヴァンデル・ポルト方程式

2つの振動子が相互作用する場合のヴァンデル・ポルト方程式があります。

この方程式は、化学や物理学、生物学などのさまざまな分野で用いられます。

2つの振動子$ (x) $と$ (y) $の間の相互作用を表すヴァンデル・ポルト方程式は次のように表されます:

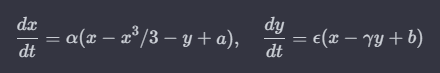
ここで、$ (a) $、$ (b) $、$ (\alpha) $、$ (\epsilon) $、$ (\gamma) $はパラメータです。

この方程式をPythonで3Dグラフ化するには、以下のようなコードを使用できます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# ヴァンデル・ポルト方程式の定義
def vanderpol_equations(x, y, alpha, epsilon, gamma, a, b):
    dx_dt = alpha * (x - (x**3)/3 - y + a)
    dy_dt = epsilon * (x - gamma * y + b)
    return dx_dt, dy_dt

# パラメータの設定
alpha = 1.0
epsilon = 1.0
gamma = 2.0
a = 1.0
b = 1.0

# 時間のステップと初期値
dt = 0.01
steps = 10000

x_vals = np.zeros(steps + 1)
y_vals = np.zeros(steps + 1)

x_vals[0], y_vals[0] = 0.1, 0.1

# 数値積分（Euler法）
for i in range(steps):
    dx, dy = vanderpol_equations(x_vals[i], y_vals[i], alpha, epsilon, gamma, a, b)
    x_vals[i + 1] = x_vals[i] + dt * dx
    y_vals[i + 1] = y_vals[i] + dt * dy

# 3Dプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x_vals, y_vals, np.arange(steps + 1))

ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Time-axis')
ax.set_title('Van der Pol Oscillator')

plt.show()

このコードは、ヴァンデル・ポルト方程式を数値的に解き、結果を3Dプロットとして表示します。

これにより、2つの振動子の相互作用が示され、その振る舞いが視覚化されます。

[実行結果]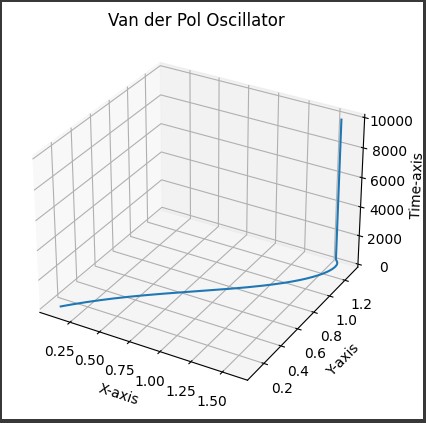

ソースコード解説

このコードは、ヴァンデル・ポルト方程式と呼ばれる非線形微分方程式を数値的に解き、その結果を3Dプロットとして表示しています。

以下がコードの詳細です。

1. ヴァンデル・ポルト方程式の定義:

  • vanderpol_equations関数では、与えられた$ (x) $と$ (y) $の値に基づいて、ヴァンデル・ポルト方程式を計算しています。
    これらの方程式は2つの微分方程式で構成されており、$ (x) $および$ (y) $の時間変化を計算します。

2. パラメータの設定:

  • ヴァンデル・ポルト方程式にはいくつかのパラメータがあり、このコードではそれらを設定しています。
    例えば、$ (\alpha) $、$ (\epsilon) $、$ (\gamma) $、$ (a) $、$ (b) $の値が与えられています。

3. 数値積分（Euler法）:

  • ループを使用して、Euler法を使って微分方程式を数値的に解いています。
    初期値$ (x = 0.1) $および$ (y = 0.1) $から始め、ループを通じて微小時間$ (dt) $だけ変化を加えて新しい$ (x) $と$ (y) $の値を計算しています。

4. 3Dプロット:

  • 最後に、Matplotlibを使用して、計算された$ (x) $と$ (y) $の値を3Dプロットとして可視化しています。
    このプロットは、$ (x) $軸と$ (y) $軸に対応する値が時間とともにどのように変化するかを示しています。

5. グラフの要素:

  • X軸は振動子$ (x) $の値を表します。
  • Y軸は振動子$ (y) $の値を表します。
  • Z軸（時間軸）は時間を表し、振動子の値が時間とともにどのように変化するかを示します。

このコードは、ヴァンデル・ポルト方程式を数値的に解き、振動子の振る舞いを視覚化しています。

振動子の振る舞いはパラメータと初期値に依存するため、これらの値を変更すると異なる振る舞いが得られます。

グラフ解説

[実行結果]

このコードは、ヴァンデル・ポルト方程式と呼ばれる非線形微分方程式を解き、その結果を3Dプロットとして表示しています。

ヴァンデル・ポルト方程式は、2つの振動子$ (x) $と$ (y) $の相互作用を表しています。

ここではEuler法を用いて微分方程式を数値的に解き、結果を3Dグラフにプロットしています。

以下はグラフの要素についての詳細です。

1. 軸の意味:

  • X軸は振動子$ (x) $の値を表します。
  • Y軸は振動子$ (y) $の値を表します。
  • Z軸（時間軸）は時間を表し、各点が時間の経過に伴って振動子の値がどのように変化するかを示しています。

2. グラフの特徴:

  • ヴァンデル・ポルト方程式は非線形であり、2つの振動子$ (x) $と$ (y) $の間の相互作用が時間とともにどのように振る舞うかを表します。
  • このグラフは、$ (x) $と$ (y) $の値が時間に応じてどのように変化するかを示しており、振動子の軌道が示されています。
    これらの軌道は、特定の初期値から始まり、振動子の相互作用によって時間の経過とともに変化します。

3. 振動の特性:

  • ヴァンデル・ポルト方程式は、非線形な振動子系の一例です。
    このグラフは、振動子の非線形な相互作用により、複雑な振る舞いを示しています。
    振動子が周期的に振動する場合や、カオス的な振る舞いを示す場合があります。

このグラフは、2つの振動子が互いに相互作用するヴァンデル・ポルト方程式の振る舞いを視覚化しており、非線形ダイナミクスが示されています。

振動子がどのように相互作用し、時間とともにどのように変化するかを理解するのに役立ちます。