サドル点

サドル点

一般的な3次元プロットでよく使用される関数としては、$z = x^2 - y^2$（サドル点）があります。

以下にPythonのmatplotlibとnumpyを用いた実装例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#x, yの値を定義
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)

#z = x^2 - y^2という関数
z = x**2 - y**2

#3D描画
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x, y, z)

# グラフ表示
plt.show()

このプログラムを実行すると、3Dグラフが表示されます。

numpyのlinspace関数を使用して$x$と$y$の範囲を定義し、meshgrid関数で$x$と$y$の座標を生成しています。

その座標の組に対して関数$ (z = x^2 - y^2) $を適用して$z$値を求め、plot_surface関数で3Dグラフに描画しています。

[実行結果]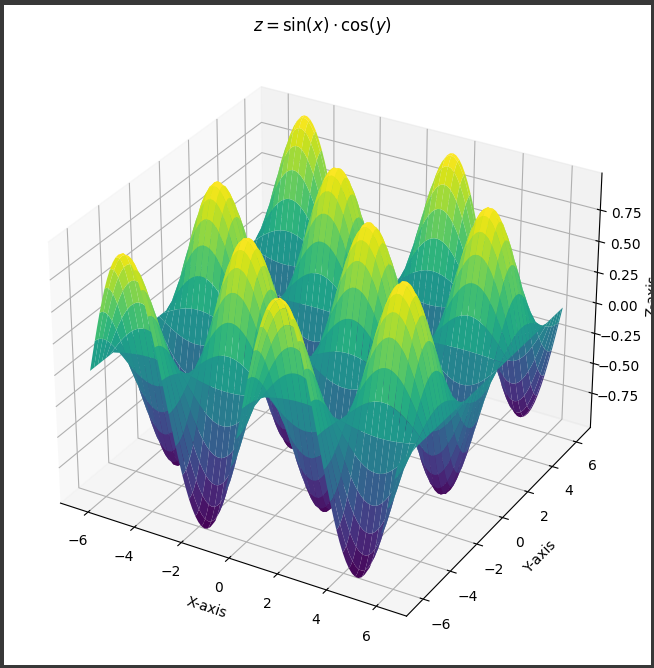

ソースコード解説

このコードは、PythonのライブラリであるNumPyとMatplotlibを使用して、$ (z = x^2 - y^2) $という関数の3Dプロットを作成しています。

以下がコードの詳細な説明です。

1. import文:

  • numpyとmatplotlib.pyplotから必要なモジュールをインポートしています。
    また、3Dプロットを作成するためのAxes3Dもインポートされています。

2. x, yの値の定義:

  • np.linspaceを使って、$-5$から$5$までの範囲を$100$個の等間隔な点で$x$と$y$軸に割り当てています。
  • meshgridを使って、$x$と$y$の格子点を作成しています。
    これにより、$x$と$y$の組み合わせのすべての点が作成されます。

3. zの計算:

  • $ (z = x^2 - y^2) $の関数を表すため、各点における$ (x^2 - y^2) $の値を計算して$z$に割り当てています。

4. 3D描画の設定:

  • plt.figure()を使用して新しい図を作成し、Axes3D関数を使用して3Dの軸を定義します。

5. ax.plot_surface:

  • plot_surfaceを使って、$x$、$y$、および対応する$z$の値を用いて表面プロットを行っています。

6. グラフの表示:

  • plt.show()を使用して、作成した3Dグラフを表示します。

このコード全体の目的は、$ (z = x^2 - y^2) $の関数を3Dプロットして、その曲面の形状を可視化することです。

$ x$と$y$が範囲内で変化すると、関数の値$z$がそれに応じて変化し、それが3次元のグラフとして表示されます。