モビウス帯

モビウス帯

モビウス帯は、帯状の特殊な幾何学的な面です。
これは通常の帯とは異なり、一周させると表面が反転してしまう特性を持っています。
この特性は、帯の表と裏の区別がなく、外側と内側が連続していることを示しています。

モビウス帯を作るには、帯の幅を持つストリップ（帯状の紙など）を取り、一端を半回転させて反対側とつなげます。

すると、通常の帯では表と裏がありますが、モビウス帯では一周しても片側だけになります。
これは3次元の空間における非常に興味深い形状であり、数学的にも重要です。

モビウス帯はトポロジー学や数学の教育において非常に興味深い対象であり、幾何学や物理学、コンピュータグラフィックスなど様々な分野で応用されています。

また、この特殊な形状は数学の美しさを示すための象徴的なものとしても知られています。

数式

一般的なモビウス帯は、次のようなパラメトリック方程式で表されます：

\begin{align*}
x(u, v) &= \left( r + v \cdot \cos\left(\frac{u}{2}\right) \right) \cdot \cos(u) \
\end{align*}
\begin{align*}
y(u, v) &= \left( r + v \cdot \cos\left(\frac{u}{2}\right) \right) \cdot \sin(u) \
\end{align*}
\begin{align*}
z(u, v) &= v \cdot \sin\left(\frac{u}{2}\right)
\end{align*}

ここで、$ (u) $は$ 0 $から$ (2\pi) $までのパラメータで、モビウス帯を一周させるための角度を表しています。

$ (v) $は帯の幅を決定するパラメータで、通常は$ (-w) $から$ (w) $の範囲で変化します。
そして$ (r) $は帯の中心からの距離を表します。

このパラメトリック方程式では、$ (u) $と$ (v) $の値の範囲によってモビウス帯の形状が変化します。

$ (u) $を$ 0 $から$ (2\pi) $まで変化させると、モビウス帯が一周しますが、一周した際に表面が反転することが特徴です。

また、$ (v) $を変化させることで帯の幅を調整することができます。

グラフ化

モビウス帯をPythonで描画するには、Matplotlibを使用して三次元プロットを行います。

以下はモビウス帯を描画するサンプルコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# モビウス帯のパラメータ
r, w = 1, 0.2  # 半径と帯の幅
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(-w, w, 50)
U, V = np.meshgrid(u, v)
X = (r + V * np.cos(U / 2)) * np.cos(U)
Y = (r + V * np.cos(U / 2)) * np.sin(U)
Z = V * np.sin(U / 2)

# 3Dプロット
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')

# グラフの設定
ax.set_title('Mobius Strip')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

このコードは、モビウス帯のパラメータを使用して3Dプロットを行い、Matplotlibで可視化します。

実行すると、モビウス帯の形状を表示するグラフが生成されます。

[実行結果]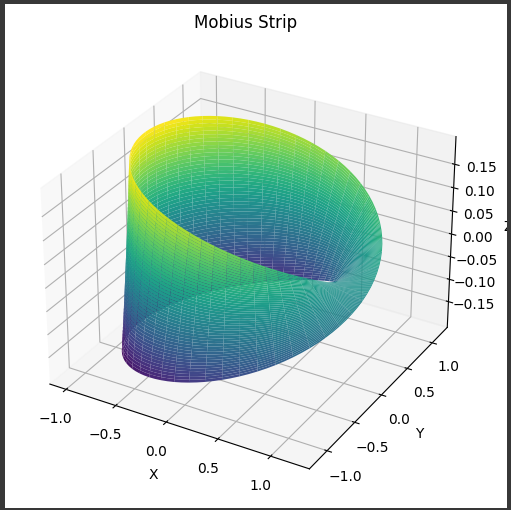

ソースコード解説

このコードは、PythonのNumPyとMatplotlibを使用してモビウス帯をプロットしています。

各行の役割や手順を見ていきましょう。

モビウス帯のパラメータ設定

1
2
3
4
5
6
7
r, w = 1, 0.2  # 半径と帯の幅
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(-w, w, 50)
U, V = np.meshgrid(u, v)
X = (r + V * np.cos(U / 2)) * np.cos(U)
Y = (r + V * np.cos(U / 2)) * np.sin(U)
Z = V * np.sin(U / 2)
  • r はモビウス帯の半径、w は帯の幅を指定します。
  • u は$0$から$2π$までを$100$等分した配列を作り、v は -w から w までを$50$等分した配列を作ります。
  • np.meshgrid を使用して、u と v のメッシュグリッドを作成します。
    これにより、U と V の2つの行列が得られます。
  • X, Y, Z は、パラメータ式を使ってモビウス帯の各点の座標を計算します。

3Dプロット

1
2
3
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
  • fig は図を表し、ax はその図上に配置される3Dサブプロットを表します。
  • ax.plot_surface で X, Y, Z のデータからモビウス帯の表面をプロットします。

グラフの設定と表示

1
2
3
4
5
6
ax.set_title('Mobius Strip')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()
  • ax.set_title, ax.set_xlabel などでグラフのタイトルや軸ラベルを設定します。
  • plt.show() でプロットを表示します。

このコードは、NumPyを使ってモビウス帯のパラメータを設定し、Matplotlibを使ってそれを3Dプロットしています。

X, Y, Z の値を変更することで、異なる半径や帯の幅のモビウス帯を描画することができます。