エルミート多項式

エルミート多項式

エルミート多項式は、物理学や数学などで使用される多項式です。

以下にエルミート多項式のグラフとPythonでの表現を示します。

エルミート多項式は次の再帰的な式で定義されます：

$$
[ H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n}(e^{-x^2}) ]
$$

これを利用して、エルミート多項式をPythonで表現し、グラフを描画します。

以下はそのコードです：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import eval_hermite

# エルミート多項式の定義
def hermite_polynomial(n, x):
    return (-1)**n * np.exp(x**2) * eval_hermite(n, x)

# グラフの描画
x = np.linspace(-5, 5, 400)
plt.figure(figsize=(8, 6))

for n in range(5):  # 最初の5つのエルミート多項式を描画
    plt.plot(x, hermite_polynomial(n, x), label=f'H_{n}(x)')

plt.xlabel('x')
plt.ylabel('H_n(x)')
plt.title('Hermite Polynomials')
plt.legend()
plt.grid(True)
plt.show()

このコードは、$-5$から$5$までの範囲で最初の5つのエルミート多項式を描画します。

[実行結果]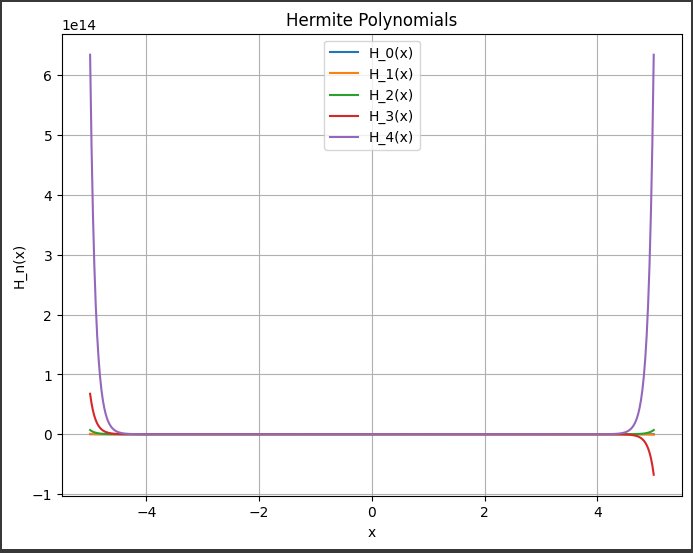

エルミート多項式は次第に複雑になり、高次の多項式ほど振動が大きくなります。

ソースコード解説

このソースコードは、Pythonを使用してエルミート多項式を計算し、グラフ化するものです。

  1. numpy、matplotlib、scipy.specialをそれぞれnp、plt、eval_hermiteとしてインポートします。
  2. hermite_polynomial関数は、エルミート多項式$ (H_n(x)) $を計算します。
    指定された次数$ (n) $と変数$ (x) $を受け取り、エルミート多項式の値を計算します。
  3. xは $-5$から$5$まで$400$個の点で等間隔になるように設定された数値を持ちます。
  4. plt.figure()で図を作成し、forループを使って最初の5つのエルミート多項式を計算・描画します。
    各多項式は異なる色で描かれ、ラベルに$ (H_n(x)) $の形式で表示されます。
  5. 軸ラベル、グラフのタイトル、凡例、グリッド線を追加して、グラフを表示します。

このコードはエルミート多項式を計算し、それらをグラフで視覚化しています。

エルミート多項式は指定された次数$ (n) $に対する関数$ (H_n(x)) $として描画され、指数関数と多項式の積として定義されています。

結果解説

このグラフは、エルミート多項式（Hermite Polynomials）を表しています。

[実行結果]

エルミート多項式は物理学や数学で重要な役割を果たす多項式で、量子力学や確率論などさまざまな分野で使用されます。

このグラフは、x軸に沿って$-5$から$5$までの範囲で、最初の5つのエルミート多項式 $ (H_0(x)) から (H_4(x)) $を示しています。

これらの多項式は、$x$の値に対する関数値として描かれています。

エルミート多項式は次数が増えるにつれて振動が増え、高次の多項式ほどより急峻な振動を示します。

また、これらの多項式は相互に直交する性質を持ち、量子力学などで波動関数を表現するのに役立ちます。