高度な数式 SciPy

高度な数式

Scipyを使用して、高度な数式を解くためのサンプルコードを提供します。

以下は、$ y = x^3 + 2x^2 - 5x + 6 $の関数を考え、その解を見つける例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
from scipy.optimize import root
import matplotlib.pyplot as plt

# 解きたい方程式の関数
def equation(x):
    return x**3 + 2*x**2 - 5*x + 6

# 初期値を設定
initial_guess = 0

# 方程式の解を求める
solution = root(equation, initial_guess)

# 解を表示
print("解:", solution.x)

# グラフ化
x_vals = np.linspace(-5, 3, 1000)
y_vals = equation(x_vals)

plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label='y = x^3 + 2x^2 - 5x + 6')
plt.scatter(solution.x, equation(solution.x), color='red', label='Solution', s=100)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Graph of the Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードは、scipy.optimize.rootを使用して方程式の解を見つけます。

また、解を求める過程をグラフに表しています。

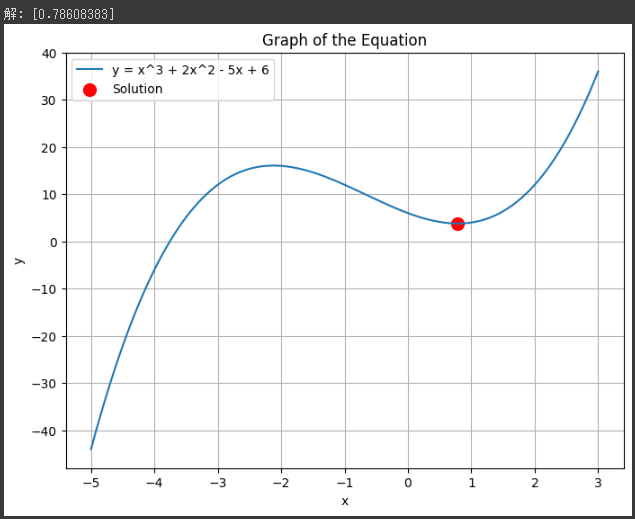
方程式の解は赤い点で示されています。

ソースコード解説

このコードは、Scipyライブラリを使用して非線形方程式を解く手順を示しています。

詳細を以下にまとめます。

ライブラリのインポート

1
2
3
import numpy as np
from scipy.optimize import root
import matplotlib.pyplot as plt

方程式の定義

1
2
def equation(x):
    return x**3 + 2*x**2 - 5*x + 6

この関数では、$ y = x^3 + 2x^2 - 5x + 6 $という非線形方程式が定義されています。

初期値の設定

1
initial_guess = 0

初期推定値を$ (x=0) $に設定しています。

方程式の解を求める

1
solution = root(equation, initial_guess)

scipy.optimize.rootを使用して、指定した方程式の解を計算します。
この場合、equation関数を与えています。

解の表示

1
print("解:", solution.x)

解をコンソールに表示します。

グラフ化

1
2
3
4
5
6
7
8
9
10
11
12
x_vals = np.linspace(-5, 3, 1000)
y_vals = equation(x_vals)

plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label='y = x^3 + 2x^2 - 5x + 6')
plt.scatter(solution.x, equation(solution.x), color='red', label='Solution', s=100)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Graph of the Equation')
plt.legend()
plt.grid(True)
plt.show()

指定した範囲の$ (x) 値$に対する方程式の$ (y) 値$を計算し、グラフ上に方程式の曲線を描画します。

また、方程式の解を赤い点で示しています。

このコード全体は、非線形方程式の数値解法とその結果の視覚化を行っています。