非線形最小二乗法（Nonlinear Least Squares） SciPy

非線形最小二乗法（Nonlinear Least Squares）

SciPyを使用して非線形最小二乗法（Nonlinear Least Squares）を実行し、その結果をグラフ化する例を示します。

具体的には、次のような非線形関数を仮定して、ノイズが混じったデータを生成し、それを元に非線形最小二乗法でパラメータを推定します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 非線形関数の定義
def nonlinear_function(x, a, b):
    return a * np.exp(b * x)

# データ生成
np.random.seed(42)
x_data = np.linspace(0, 2, 100)
y_data = 2.5 * np.exp(1.2 * x_data) + 0.2 * np.random.normal(size=len(x_data))

# 非線形最小二乗法でパラメータ推定
params, covariance = curve_fit(nonlinear_function, x_data, y_data)

# 推定されたパラメータ
a_fit, b_fit = params

# 推定した関数をプロット
y_fit = nonlinear_function(x_data, a_fit, b_fit)

# グラフ化
plt.scatter(x_data, y_data, label='実際のデータ')
plt.plot(x_data, y_fit, 'r', label='非線形最小二乗法によるフィット')
plt.title('非線形最小二乗法によるフィット')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

この例では、非線形関数 $a * exp(b * x)$ に従うデータを生成し、curve_fit 関数を使用して非線形最小二乗法によりパラメータ $a$ と $b$ を推定しています。

結果をグラフで可視化しています。

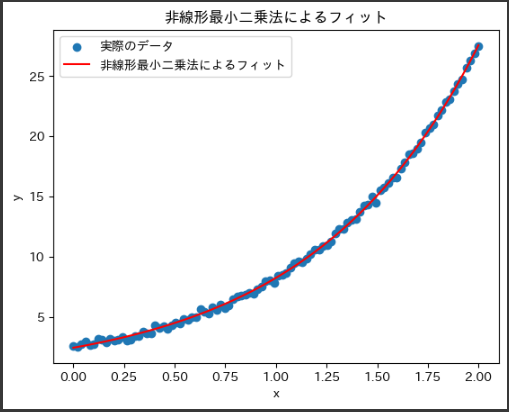
このコードを実行すると、元データと非線形最小二乗法によってフィットされた曲線が可視化されます。

データにノイズが含まれているため、フィットされた曲線が元データによく適合していることが期待されます。

ソースコード解説

以下にソースコードの各部分の詳細な説明をします。

1. import numpy as np:

  • NumPy ライブラリを np としてインポートしています。
    NumPyは数値計算や行列演算を行うための基本的なライブラリです。

2. import matplotlib.pyplot as plt:

  • Matplotlib ライブラリの pyplot モジュールを plt としてインポートしています。
    Matplotlibはグラフ描画ライブラリで、pyplot モジュールは簡単なプロットを作成するための機能を提供します。

3. from scipy.optimize import curve_fit:

  • SciPy ライブラリから curve_fit 関数をインポートしています。
    curve_fit 関数は、非線形最小二乗法によって関数のパラメータを推定するために使用されます。

4. 非線形関数の定義:

  • nonlinear_function は非線形関数を表しています。
    この例では、指数関数 $a * exp(b * x)$ が使われています。
    関数はパラメータ $a$ と $b$ を受け取り、$a * np.exp(b * x)$ を返します。

5. データ生成:

  • np.linspace(0, 2, 100) を用いて、0から2までの範囲を等間隔に区切った x_data を生成します。
  • 2.5 * np.exp(1.2 * x_data) + 0.2 * np.random.normal(size=len(x_data)) により、ノイズを加えた非線形なデータ y_data を生成します。
    np.random.normal は平均0、標準偏差0.2の正規分布に従うノイズです。

6. 非線形最小二乗法:

  • curve_fit(nonlinear_function, x_data, y_data) で非線形最小二乗法を実行し、関数 nonlinear_function のパラメータをデータにフィットさせます。
    結果として、params には推定されたパラメータが、covariance には共分散行列が格納されます。

7. 推定されたパラメータ:

  • params から得られた推定されたパラメータ a_fit と b_fit を抽出します。

8. 推定した関数をプロット:

  • 推定されたパラメータを用いて、元の非線形関数を再度計算し、y_fit として保存します。

9. グラフ化:

  • plt.scatter を用いて元のデータを散布図としてプロットします。
  • plt.plot を用いて、非線形最小二乗法によって得られたフィットした曲線をプロットします。
    色は赤色 ('r') に設定されています。
  • タイトル、x軸ラベル、y軸ラベルを設定します。
  • plt.legend() で凡例を表示します。
  • plt.show() でグラフを表示します。

このプログラムを実行すると、元のデータと非線形最小二乗法によってフィットされた曲線が同じグラフ上に表示されます。

これにより、非線形最小二乗法がデータに適切に適合しているかを可視化できます。

結果解説

上記のコードで生成されるグラフは、非線形最小二乗法を使用してフィットされた曲線と元のデータを可視化したものです。

以下にグラフの要素について詳しく説明します。

1. 散布図（Scatter plot）:

  • データ生成時に生成されたノイズの影響を受けた実際のデータ点が散布図として表示されています。

2. フィットされた曲線（Fitted Curve）:

  • 赤い線が非線形最小二乗法によって推定された非線形関数の曲線です。
    この曲線は、データに最もよく適合するようにパラメータ a と b が調整された結果です。

3. タイトル（Title）:

  • グラフのタイトルは「非線形最小二乗法によるフィット」となっています。

4. x軸とy軸（X-axis and Y-axis）:

  • x軸は x_data で、y軸は y_data および y_fit で、それぞれデータのx座標とy座標を表しています。

5. 凡例（Legend）:

  • グラフには凡例が表示されており、散布図が「実際のデータ」、赤い線が「非線形最小二乗法によるフィット」を示しています。

このグラフから、非線形最小二乗法が元のデータに対して適切な曲線をフィットしていることがわかります。

データの散らばりに対応して、赤い線がデータの傾向を捉えています。

最小二乗法によって得られたパラメータにより、元の非線形関数が近似され、それが赤い線として表示されています。