制約条件を持つ最適化問題 scipy

制約条件を持つ最適化問題

制約条件を持つ最適化問題を解くためには、scipy.optimizeモジュールを使用することが一般的です。

以下は、scipyを使用して制約条件のある最適化問題を解くサンプルコードです。

この例では、制約条件付きの2次元目的関数を最小化する問題を考えます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 目的関数の定義
def objective(x):
    return x[0]**2 + x[1]**2

# 制約条件
def constraint(x):
    return x[0] + x[1] - 1

# 初期値
x0 = np.array([0.5, 0.5])

# 制約条件付き最適化
constraints = {'type': 'eq', 'fun': constraint}
result = minimize(objective, x0, constraints=constraints)

# 結果の表示
print("最適な解:", result.x)
print("最小値:", result.fun)

[実行結果]

グラフ化

次に、結果をグラフ化してみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 目的関数を等高線プロット
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2

plt.contour(X, Y, Z, levels=np.logspace(-1, 2, 10), cmap='viridis')

# 制約条件をプロット
plt.plot(x, 1 - x, '-r', label='x + y = 1')

# 最適解をプロット
plt.plot(result.x[0], result.x[1], 'ro', label='最適解')

plt.xlabel('x')
plt.ylabel('y')
plt.title('Constrained Optimization')
plt.legend()
plt.show()

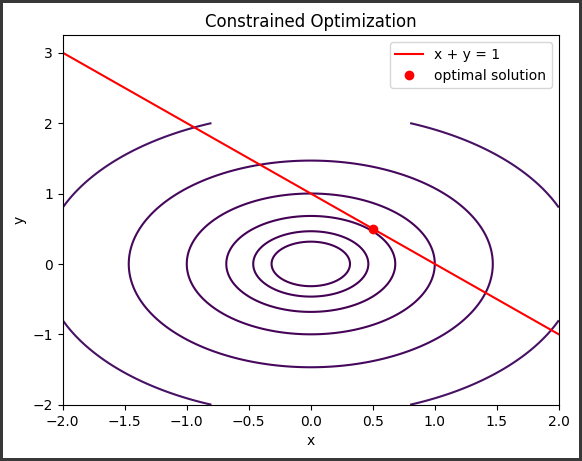
このコードでは、2次元の目的関数を最小化しながら、制約条件 x + y = 1 を満たす最適解を求めています。

結果は等高線プロットとして表示され、最適解は赤い点で示されます。

なお、制約条件のある最適化問題は様々な種類があり、それぞれ異なるアプローチが必要です。

上記の例は一般的なサンプルであり、実際の問題に応じて適切なアルゴリズムや制約条件の設計が必要です。

[実行結果]