物流 scikit-learn

8月 1, 2023

物流

物流の例題として、「ある企業が複数の倉庫から商品を顧客へ配送する場合の最適なルート設計」を考えてみましょう。

この問題は、倉庫と顧客の位置情報を元に、最短距離を通るルートを見つける問題として解釈できます。

ここでは、scikit-learnのKMeansクラスタリングアルゴリズムを使用して、倉庫と顧客をクラスタリングし、それぞれのクラスタの重心（倉庫の位置）とクラスタ内の各顧客との距離を求める方法を示します。

なお、本来の物流問題はより複雑であり、現実的なソリューションにはさまざまな要素（ルートの容量、交通状況、顧客の要求など）が含まれますが、ここでは単純化した例題を取り扱います。

以下はPythonコードでの例示です。

なお、numpyとmatplotlibも使用しますので、事前にインストールしてください。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# データの作成（仮想的な倉庫と顧客の位置情報）
np.random.seed(0)
n_warehouses = 3
n_customers = 10
data = np.vstack((
    np.random.rand(n_warehouses, 2) * 10,  # 倉庫の位置情報 (x, y)
    np.random.rand(n_customers, 2) * 10   # 顧客の位置情報 (x, y)
))

# KMeansクラスタリング
n_clusters = n_warehouses
kmeans = KMeans(n_clusters=n_clusters)
kmeans.fit(data)
centers = kmeans.cluster_centers_  # 倉庫の位置

# グラフ化
plt.scatter(data[:, 0], data[:, 1], c=kmeans.labels_, cmap='rainbow')
plt.scatter(centers[:, 0], centers[:, 1], marker='X', s=200, c='black', label='Warehouses')
plt.legend()
plt.title('Warehouse Location and Customer Clustering')
plt.xlabel('X-coordinate')
plt.ylabel('Y-coordinate')
plt.grid(True)
plt.show()

このコードでは、倉庫と顧客の位置情報をランダムに生成し、KMeansアルゴリズムを使用してクラスタリングしています。

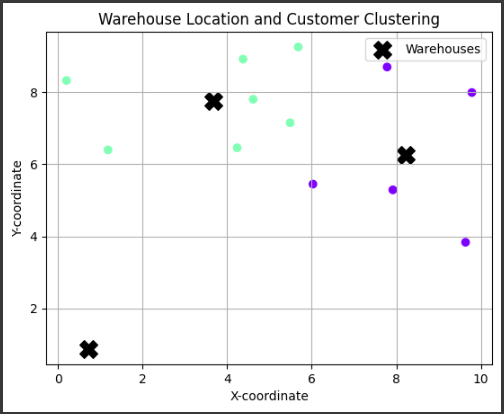
グラフでは、倉庫と顧客を異なる色でプロットし、倉庫の位置を「X」マークで示しています。

[実行結果]

ソースコード解説

このコードは、Pythonを使用して物流の例題を扱い、scikit-learnとmatplotlibを使ってデータのクラスタリングとグラフ化を行っています。

以下、各部分の詳細な説明を行います。

1. ライブラリのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

numpyは数値計算を行う際の基本的なライブラリです。
matplotlib.pyplotはデータの可視化のためのライブラリで、グラフのプロットに使用します。
sklearn.cluster.KMeansは、scikit-learnライブラリのKMeansクラスタリングアルゴリズムを提供します。

2. データの作成:

np.random.seed(0)
n_warehouses = 3
n_customers = 10
data = np.vstack((
    np.random.rand(n_warehouses, 2) * 10,  # 倉庫の位置情報 (x, y)
    np.random.rand(n_customers, 2) * 10   # 顧客の位置情報 (x, y)
))

np.random.seed(0)は、ランダムなデータを生成する際に再現性を持たせるための乱数シードを設定しています。
n_warehousesは倉庫の数を表し、n_customersは顧客の数を表します。
np.random.rand(n_warehouses, 2) * 10とnp.random.rand(n_customers, 2) * 10は、それぞれ倉庫と顧客の位置情報を2次元のランダムな座標（x, y）で生成しています。
* 10は生成される座標を0から10の範囲にスケーリングするためです。

3. KMeansクラスタリング:

n_clusters = n_warehouses
kmeans = KMeans(n_clusters=n_clusters)
kmeans.fit(data)
centers = kmeans.cluster_centers_  # 倉庫の位置

n_clustersには倉庫の数が設定されています。
これは、KMeansアルゴリズムがデータを指定されたクラスタ数に分割するために使用されます。
KMeans(n_clusters=n_clusters)でKMeansクラスタリングのインスタンスを作成し、fitメソッドでデータをクラスタリングします。
kmeans.cluster_centers_は、クラスタの重心（倉庫の位置）を表すNumPy配列として取得されます。

4. グラフ化:

plt.scatter(data[:, 0], data[:, 1], c=kmeans.labels_, cmap='rainbow')
plt.scatter(centers[:, 0], centers[:, 1], marker='X', s=200, c='black', label='Warehouses')
plt.legend()
plt.title('Warehouse Location and Customer Clustering')
plt.xlabel('X-coordinate')
plt.ylabel('Y-coordinate')
plt.grid(True)
plt.show()

plt.scatter(data[:, 0], data[:, 1], c=kmeans.labels_, cmap='rainbow')は、倉庫と顧客の位置情報を散布図としてプロットします。
c=kmeans.labels_により、各データポイントのクラスタラベルを表す色が自動的に割り当てられます。
plt.scatter(centers[:, 0], centers[:, 1], marker='X', s=200, c='black', label='Warehouses')は、倉庫の位置情報を「X」マークでプロットします。
plt.legend()で凡例を表示します。
ここでは、「Warehouses」というラベルを使っています。
plt.title('Warehouse Location and Customer Clustering')、plt.xlabel('X-coordinate')、plt.ylabel('Y-coordinate')は、それぞれグラフのタイトルとx軸、y軸のラベルを設定します。
plt.grid(True)でグリッドを表示します。
plt.show()は、作成したグラフを表示します。

これにより、倉庫と顧客の位置情報をクラスタリングして、それぞれの位置を可視化することができます。

結果解説

上記の例題では、3つの倉庫と10人の顧客の位置情報を用いてKMeansクラスタリングを行いました。
結果として得られたグラフを解釈します。

グラフでは、データポイントが2次元空間上にプロットされており、異なる色で示されています。

ここで、色の違いはKMeansによって割り当てられたクラスタを表しています。

クラスタ数は倉庫の数に設定しましたので、3つのクラスタがあります。

また、Xマークで示されたデータポイントが各クラスタの中心点を表しています。

これは倉庫の位置を示しており、3つの倉庫がそれぞれのクラスタ内で最も重要な位置を占めていることが分かります。

結果の解釈:

1. 倉庫の位置:

Xマークで示されている3つの点が、倉庫の位置を表しています。
これらの点は、クラスタリングによってデータの中心に近い位置に配置されているため、最適な倉庫の位置となります。
これらの倉庫が、顧客への商品配送の拠点として選ばれるでしょう。

2. 顧客の位置:

グラフ上のXマーク以外のデータポイントは、顧客の位置を表しています。
これらの点は、それぞれ最も近い倉庫に配送されることになります。
異なる色のクラスタに属する顧客は、異なる倉庫に配送されることが予想されます。

この結果を元に、企業は倉庫と顧客の位置を適切に設計し、各倉庫からの最適なルートを計画することができます。

ただし、実際の物流問題ではさらに多くの要素を考慮する必要があるため、より複雑なアルゴリズムや手法を用いて最適解を求めることが一般的です。