ファシリティ配置問題 SciPy

ファシリティ配置問題（１次元）

ファシリティ配置問題は、一般的には、特定の制約の下で最適な場所に施設を配置する問題です。

ここでは、シンプルな例として、一次元の空間に存在する複数の都市に対して、最適な場所に施設を配置する問題を考えてみましょう。

目標は、全ての都市から施設までの距離の合計を最小化することです。

この問題は、PythonのSciPyライブラリを使用して解くことができます。

以下にそのコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 都市の位置
cities = np.array([2, 5, 11, 16, 20, 23, 27, 30])

# 目的関数（全ての都市から施設までの距離の合計）
def objective(x):
    return np.sum(np.abs(cities - x))

# 初期値
x0 = np.array([15])

# 最適化
result = minimize(objective, x0, method='Nelder-Mead')

# 結果の表示
print("Optimal location: ", result.x)

# グラフの描画
plt.figure(figsize=(8, 4))
plt.plot(cities, [1]*len(cities), 'ro')
plt.plot(result.x, [1], 'bo')
plt.yticks([])
plt.grid(True)
plt.show()

このコードでは、都市の位置を表す配列citiesを定義し、目的関数objectiveを定義しています。

目的関数は、施設の位置xから各都市までの距離の絶対値の合計を計算します。

次に、初期値x0を設定し、SciPyのminimize関数を使用して目的関数を最小化します。

最適化の結果は、result.xに格納されます。

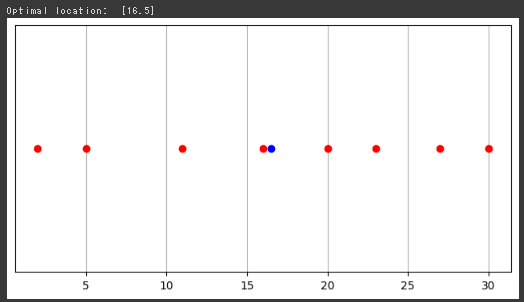
最後に、都市の位置と最適な施設の位置をグラフに描画します。

赤い点が都市の位置を、青い点が最適な施設の位置を示しています。

[実行結果]

ファシリティ配置問題（２次元）

二次元空間に存在する複数の都市に対して施設を配置する問題も同様に解くことができます。

ここでは、都市の座標を2次元のnumpy配列で表現し、目的関数もそれに合わせて変更します。

以下にそのPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 都市の位置
cities = np.array([[2, 3], [5, 1], [1, 6], [8, 6], [7, 4], [4, 7], [6, 2], [3, 4]])

# 目的関数（全ての都市から施設までの距離の合計）
def objective(x):
    return np.sum(np.sqrt(np.sum((cities - x)**2, axis=1)))

# 初期値
x0 = np.array([5, 5])

# 最適化
result = minimize(objective, x0, method='Nelder-Mead')

# 結果の表示
print("Optimal location: ", result.x)

# グラフの描画
plt.figure(figsize=(8, 8))
plt.plot(cities[:, 0], cities[:, 1], 'ro')
plt.plot(result.x[0], result.x[1], 'bo')
plt.grid(True)
plt.show()

このコードでは、都市の位置を表す2次元配列citiesを定義し、目的関数objectiveを定義しています。

目的関数は、施設の位置xから各都市までのユークリッド距離の合計を計算します。

次に、初期値x0を設定し、SciPyのminimize関数を使用して目的関数を最小化します。

最適化の結果は、result.xに格納されます。

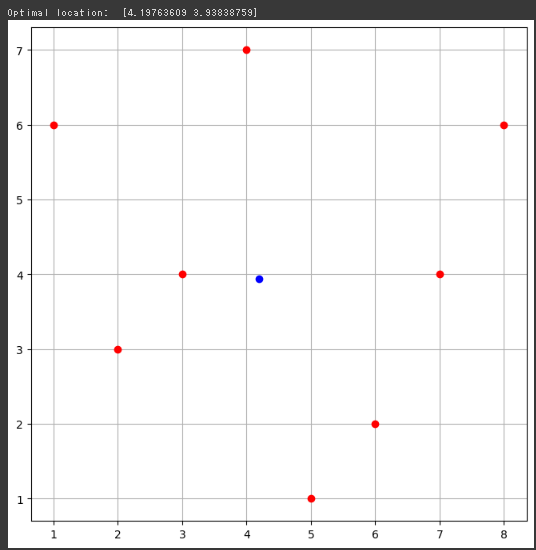
最後に、都市の位置と最適な施設の位置をグラフに描画します。

赤い点が都市の位置を、青い点が最適な施設の位置を示しています。

[実行結果]

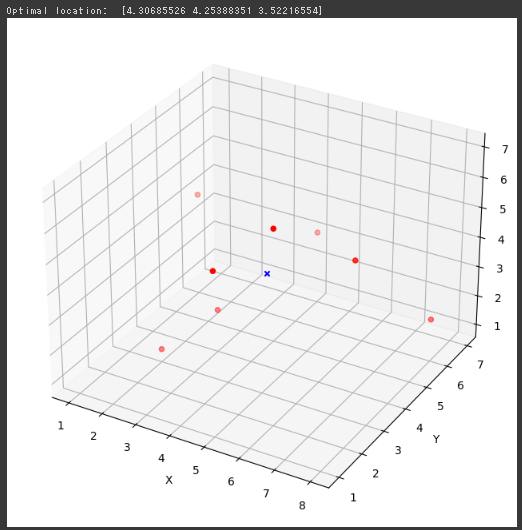
ファシリティ配置問題（３次元）

三次元空間に存在する複数の都市に対して施設を配置する問題も同様に解くことできます。

ここでは、都市の座標を3次元のnumpy配列で表現し、目的関数もそれに合わせて変更します。

以下にそのPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
from scipy.optimize import minimize
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

# 都市の位置
cities = np.array([[2, 3, 1], [5, 1, 6], [1, 6, 4], [8, 6, 2], [7, 4, 5], [4, 7, 3], [6, 2, 7], [3, 4, 2]])

# 目的関数（全ての都市から施設までの距離の合計）
def objective(x):
    return np.sum(np.sqrt(np.sum((cities - x)**2, axis=1)))

# 初期値
x0 = np.array([5, 5, 5])

# 最適化
result = minimize(objective, x0, method='Nelder-Mead')

# 結果の表示
print("Optimal location: ", result.x)

# グラフの描画
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(cities[:, 0], cities[:, 1], cities[:, 2], c='r', marker='o')
ax.scatter(result.x[0], result.x[1], result.x[2], c='b', marker='x')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

このコードでは、都市の位置を表す配列citiesを定義し、目的関数objectiveを定義しています。

目的関数は、施設の位置xから各都市までのユークリッド距離の合計を計算します。

次に、初期値x0を設定し、SciPyのminimize関数を使用して目的関数を最小化します。

最適化の結果は、result.xに格納されます。

最後に、都市の位置と最適な施設の位置を3Dグラフに描画します。

赤い点が都市の位置を、青い点が最適な施設の位置を示しています。

[実行結果]