線形計画問題 SciPy

線形計画問題

経済に関する最適化問題の一例として、線形計画問題（Linear Programming Problem, LP）を考えます。

この問題では、目的関数を最大化（または最小化）するように、制約条件のもとで変数を選択します。

ここでは、生産計画問題を例に取り上げます。

問題設定：

ある工場では、製品Aと製品Bを生産しています。製品Aの利益は100ドル、製品Bの利益は150ドルです。

🔹製品Aを1つ生産するのに、原料Xが1単位、原料Yが3単位必要です。
🔹製品Bを1つ生産するのに、原料Xが2単位、原料Yが1単位必要です。
🔹工場には、原料Xが4単位、原料Yが6単位しかありません。

この制約条件のもとで、利益を最大化する生産計画を求めます。

解法

この問題をSciPyを使って解くために、scipy.optimize.linprog関数を使用します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
from scipy.optimize import linprog

# 目的関数の係数 (最大化のためにマイナスにする)
c = np.array([-100, -150])

# 制約条件の係数
A = np.array([[1, 2], [3, 1]])
b = np.array([4, 6])

# 変数の範囲 (0以上)
x_bounds = (0, None)
y_bounds = (0, None)

# 最適化問題を解く
res = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, y_bounds], method='highs')

print(res)

実行すると、最適な生産計画が得られます。

res.xには、製品Aと製品Bの最適な生産量が格納されています。

res.funには、最大化された利益の値が格納されています（マイナスになっているので、正の値に戻す必要があります）。

[実行結果]
        message: Optimization terminated successfully. (HiGHS Status 7: Optimal)
        success: True
         status: 0
            fun: -339.9999999999999
              x: [ 1.600e+00  1.200e+00]
            nit: 2
          lower:  residual: [ 1.600e+00  1.200e+00]
                 marginals: [ 0.000e+00  0.000e+00]
          upper:  residual: [       inf        inf]
                 marginals: [ 0.000e+00  0.000e+00]
          eqlin:  residual: []
                 marginals: []
        ineqlin:  residual: [ 0.000e+00  0.000e+00]
                 marginals: [-7.000e+01 -1.000e+01]
 mip_node_count: 0
 mip_dual_bound: 0.0
        mip_gap: 0.0

各要素の詳細は以下の通りです。

  • message:
    最適化が正常に終了したことを示すメッセージです。
    HiGHSソルバーが最適解を見つけたことを示しています。
  • success:
    最適化が成功したかどうかを示すブール値です。
    Trueは成功を意味します。
  • status:
    最適化の終了ステータスを示す整数です。
    0は成功を意味します。
  • fun:
    目的関数の最適値です。
    この問題では、最大化を行っているため、値はマイナスになっています。
    実際の最大利益は、この値の正の逆数である340ドルです。
  • x:
    最適解を示す配列です。
    この場合、製品Aの最適生産量は1.6個、製品Bの最適生産量は1.2個です。
  • nit:
    反復回数です。
    この問題では、2回の反復で最適解が見つかりました。
  • lower, upper, eqlin, ineqlin:
    これらは、最適化問題の制約条件に関する情報を提供します。
    residualは制約条件の残差を示し、marginalsは制約条件の影響を示します。
    この問題では、ineqlinのmarginalsが-70と-10であり、これは制約条件が目的関数に与える影響を示しています。
  • mip_node_count, mip_dual_bound, mip_gap:
    これらはMixed Integer Programming (MIP)問題に関する情報ですが、この問題ではMIPではないため、関連性がありません。

この結果から、最適化問題が正常に解決され、最適な生産計画が得られたことがわかります。

製品Aの最適生産量は1.6個、製品Bの最適生産量は1.2個で、最大利益は340ドルです。

グラフ化

この生産計画問題の結果をグラフ化して説明するために、matplotlibを使用します。

グラフには、原料Xと原料Yの制約条件を示す直線と、最適な生産計画を示す点を描画します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt

# 制約条件の直線を描画する関数
def plot_constraints(x):
    y1 = (4 - x) / 2
    y2 = 6 - 3 * x
    return y1, y2

# xの範囲を設定
x = np.linspace(0, 4, 100)

# 制約条件の直線を計算
y1, y2 = plot_constraints(x)

# 最適な生産計画を計算
optimal_x = res.x[0]
optimal_y = res.x[1]

# グラフを描画
plt.plot(x, y1, label="1x + 2y <= 4")
plt.plot(x, y2, label="3x + 1y <= 6")
plt.xlim(0, 4)
plt.ylim(0, 4)
plt.xlabel("Product A")
plt.ylabel("Product B")
plt.legend()

# 最適な生産計画を示す点を描画
plt.plot(optimal_x, optimal_y, 'ro', label="Optimal Production Plan")
plt.annotate(f"({optimal_x:.2f}, {optimal_y:.2f})", (optimal_x + 0.1, optimal_y - 0.2))

plt.show()
[実行結果]

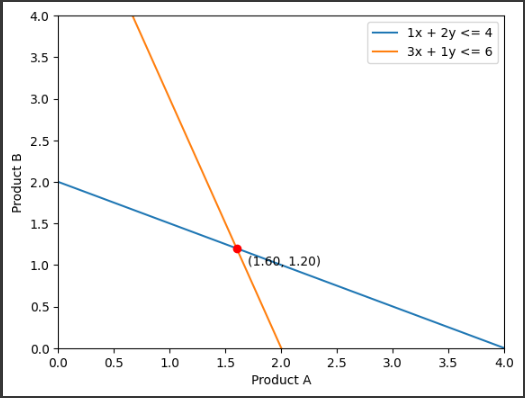
このグラフでは、x軸が製品Aの生産量、y軸が製品Bの生産量を表しています。

青い線は原料Xの制約条件$（1x + 2y <= 4）$を示し、オレンジの線は原料Yの制約条件$（3x + 1y <= 6）$を示しています。

赤い点は最適な生産計画を示しており、その座標は最適な生産量（製品Aと製品B）です。

このグラフから、最適な生産計画が制約条件の範囲内で利益を最大化することがわかります。