最小ジャーク（最小急加速度）軌道計画 CVXPY

最小ジャーク（最小急加速度）軌道計画

ロボットの運動計画において、一般的な凸最適化問題の例として、最小ジャーク（最小急加速度）軌道計画があります。

この問題では、ロボットが始点から終点までの間で、急加速度（jerk）を最小化する軌道を見つけることが目的です。

以下に、CVXPYを使用して最小ジャーク軌道計画問題を解くPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import cvxpy as cp
import numpy as np

# パラメータ設定
N = 100  # 時間ステップ数
dt = 0.1  # 時間ステップの間隔
start_pos = np.array([0, 0])  # 始点
end_pos = np.array([1, 1])  # 終点

# 変数の定義
pos = cp.Variable((N, 2))
vel = cp.Variable((N, 2))
acc = cp.Variable((N, 2))
jerk = cp.Variable((N - 1, 2))

# 制約条件の設定
constraints = [
    pos[0] == start_pos,
    pos[-1] == end_pos,
    vel[0] == 0,
    vel[-1] == 0,
    acc[0] == 0,
    acc[-1] == 0,
]

for i in range(N - 1):
    constraints += [
        pos[i + 1] == pos[i] + vel[i] * dt + 0.5 * acc[i] * dt ** 2,
        vel[i + 1] == vel[i] + acc[i] * dt,
        acc[i + 1] == acc[i] + jerk[i] * dt,
    ]

# 目的関数の定義
objective = cp.Minimize(cp.sum_squares(jerk))

# 最適化問題の定義
prob = cp.Problem(objective, constraints)

# 最適化問題の解決
prob.solve()

# 結果の表示
print("最適な軌道の位置:\n", pos.value)
print("最適な軌道の速度:\n", vel.value)
print("最適な軌道の加速度:\n", acc.value)
print("最適な軌道の急加速度:\n", jerk.value)

このコードは、ロボットが2次元空間で始点から終点まで移動する際の最小ジャーク軌道を計算します。

CVXPYを使用して、制約条件を満たす最適な軌道を見つけることができます。

コードを実行すると最適な軌道の位置、速度、加速度、および急加速度が出力されます。

[実行結果]
最適な軌道の位置:
 [[7.01960674e-18 7.01960674e-18]
 [1.79198290e-17 1.79198290e-17]
 [3.00030003e-05 3.00030003e-05]
 
 （・・・略・・・）
 
 [9.99851822e-01 9.99851822e-01]
 [9.99969997e-01 9.99969997e-01]
 [1.00000000e+00 1.00000000e+00]]
最適な軌道の速度:
 [[3.56938295e-17 3.56938295e-17]
 [7.68980513e-17 7.68980513e-17]
 [6.00060006e-04 6.00060006e-04]

 （・・・略・・・）

 [1.76344165e-03 1.76344165e-03]
 [6.00060006e-04 6.00060006e-04]
 [3.52956039e-17 3.52956039e-17]]
最適な軌道の加速度:
 [[ 6.21202559e-17  6.21202559e-17]
 [ 6.00060006e-03  6.00060006e-03]
 [ 1.16338164e-02  1.16338164e-02]

 （・・・略・・・）

 [-1.16338164e-02 -1.16338164e-02]
 [-6.00060006e-03 -6.00060006e-03]
 [-5.79512950e-17 -5.79512950e-17]]
最適な軌道の急加速度:
 [[ 0.060006    0.060006  ]
 [ 0.05633216  0.05633216]
 [ 0.05273408  0.05273408]

 （・・・略・・・）

 [ 0.05273408  0.05273408]
 [ 0.05633216  0.05633216]
 [ 0.060006    0.060006  ]]

グラフ化

以下のPythonコードは、上記の最小ジャーク軌道計画問題の結果をグラフ化します。

Matplotlibライブラリを使用して、位置、速度、加速度、および急加速度のグラフを描画します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import matplotlib.pyplot as plt

# グラフの描画
fig, axes = plt.subplots(4, 1, figsize=(10, 20))

# 位置グラフ
axes[0].plot(pos.value[:, 0], pos.value[:, 1], marker='o', markersize=3)
axes[0].set_title('Position')
axes[0].set_xlabel('X')
axes[0].set_ylabel('Y')

# 速度グラフ
axes[1].plot(np.arange(N), vel.value[:, 0], label='X')
axes[1].plot(np.arange(N), vel.value[:, 1], label='Y')
axes[1].set_title('Velocity')
axes[1].set_xlabel('Time step')
axes[1].set_ylabel('Velocity')
axes[1].legend()

# 加速度グラフ
axes[2].plot(np.arange(N), acc.value[:, 0], label='X')
axes[2].plot(np.arange(N), acc.value[:, 1], label='Y')
axes[2].set_title('Acceleration')
axes[2].set_xlabel('Time step')
axes[2].set_ylabel('Acceleration')
axes[2].legend()

# 急加速度グラフ
axes[3].plot(np.arange(N - 1), jerk.value[:, 0], label='X')
axes[3].plot(np.arange(N - 1), jerk.value[:, 1], label='Y')
axes[3].set_title('Jerk')
axes[3].set_xlabel('Time step')
axes[3].set_ylabel('Jerk')
axes[3].legend()

plt.tight_layout()
plt.show()

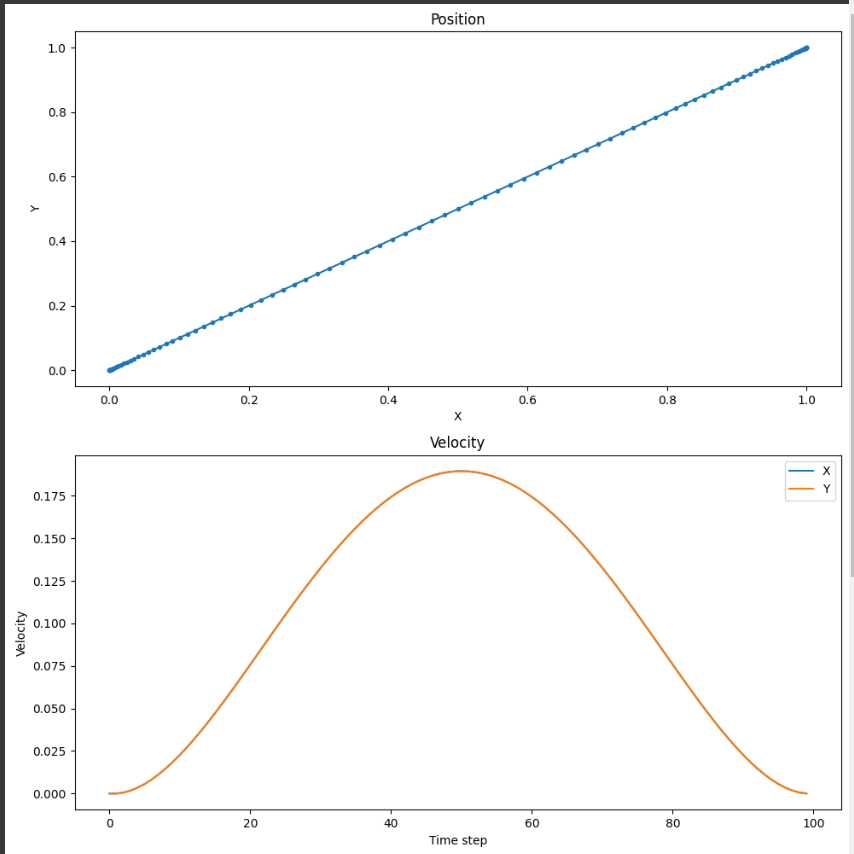
このコードによって生成されるグラフは、以下の情報を示しています。

  1. 位置グラフ: ロボットが始点から終点まで移動する軌道を示しています。
    　軌道は滑らかで、急激な変化がないことがわかります。

  2. 速度グラフ: ロボットの速度が時間ステップに応じてどのように変化するかを示しています。
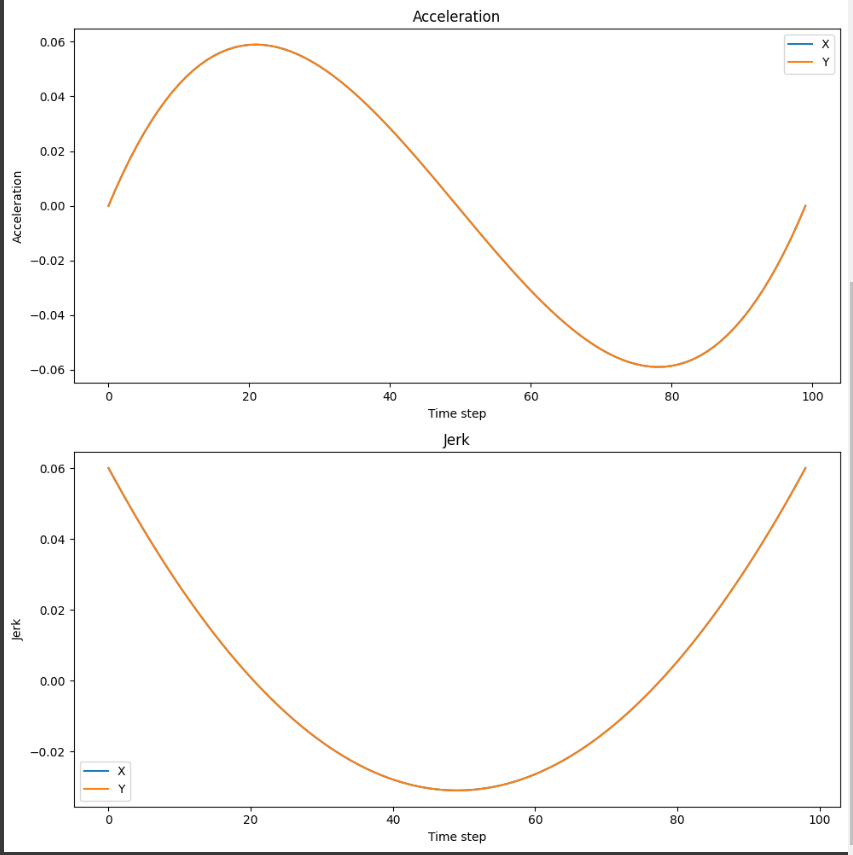
    　速度は始点と終点でゼロになり、途中で最大値に達します。

  3. 加速度グラフ: ロボットの加速度が時間ステップに応じてどのように変化するかを示しています。
    　加速度は始点と終点でゼロになり、途中で最大値および最小値に達します。

  4. 急加速度グラフ: ロボットの急加速度（jerk）が時間ステップに応じてどのように変化するかを示しています。
    　このグラフは、最小ジャーク軌道計画問題の目的関数が最小化されていることを示しています。

これらのグラフは、最小ジャーク軌道計画問題が適切に解決され、ロボットが滑らかな軌道で始点から終点まで移動できることを示しています。

[実行結果]


上記のグラフに基づいて、最小ジャーク軌道計画問題が適切に解決されたことが確認できます。

ロボットは、急加速度（jerk）を最小化することで、滑らかな軌道をたどりながら始点から終点まで移動できます。

この結果は、ロボットの運動性能を向上させ、衝突や不必要な振動を回避するのに役立ちます。

最小ジャーク軌道計画は、ロボットアームや自動運転車など、さまざまなロボットアプリケーションで使用されています。

この問題を解決することで、ロボットは効率的かつ安全に目標位置に到達できます。

今後のステップとして、他の制約条件や目的関数を追加して、問題をさらに複雑にすることができます。

例えば、障害物を回避する制約や、<>エネルギー消費を最小化する目的関数を追加することができます。

これにより、より現実的なシナリオでロボットの運動計画を最適化することができます。