1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
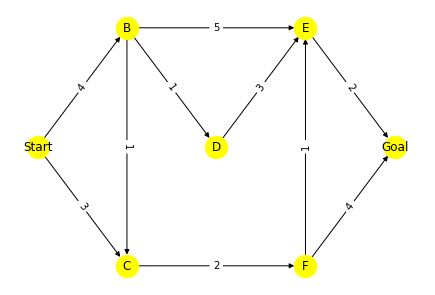
nodes = {
'Start':{'edge':{'B':4, 'C':3},
'cost':0},
'B': {'edge':{'C':1, 'D':1, 'E':5},
'cost':float('inf')},
'C': {'edge':{'F':2},
'cost':float('inf')},
'D': {'edge':{'E':3},
'cost':float('inf')},
'E': {'edge':{'Goal':2},
'cost':float('inf')},
'F': {'edge':{'E':1, 'Goal':4},
'cost':float('inf')},
'Goal': {'edge':{},
'cost':float('inf')}
}
import heapq
q = []
heapq.heappush(q, (0, 'Start', 'Start'))
while len(q):
d = heapq.heappop(q)
min_node_name = d[1]
path = d[2]
if min_node_name == 'Goal':
print('解:最小コストは', nodes['Goal']['cost'])
print('経路:', path)
break
for dst, cost in nodes[min_node_name]['edge'].items():
if nodes[dst]['cost'] > nodes[min_node_name]['cost'] + cost:
nodes[dst]['cost'] = nodes[min_node_name]['cost'] + cost
heapq.heappush(q, (nodes[dst]['cost'], dst, path + ' → ' + dst))
|