ダイクストラ法＋ヒープキュー（最短経路問題）

ダイクストラ法＋ヒープキュー

前回記事では、ダイクストラ法 を使って最短経路問題を解きました。

今回は、ヒープキュー を使って処理をより効率的にしていきます。

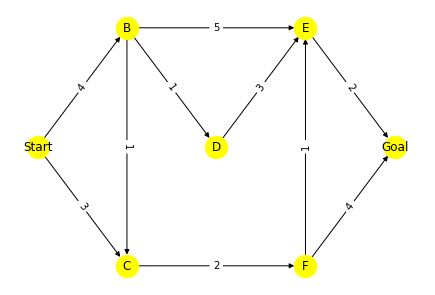
グラフは前回同様のものを使います。

[グラフ]

ソースコード

ヒープキュー は、格納されているデータの中から 一番小さなもの を効率よく取り出せるキューです。

ダイクストラ法 の処理の中で、一番小さなコストの頂点を探すときに ヒープキュー（heapq） を使います。

（入力データの形式は前回記事と同様です）

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#---------- 入力例 ----------
nodes = {                                   # ノード情報
    'Start':{'edge':{'B':4, 'C':3},         # 隣の頂点までのコスト（頂点名:コスト）
             'cost':0},                     # 頂点Startまでの最小コスト
    'B':    {'edge':{'C':1, 'D':1, 'E':5},  # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Bまでの最小コスト
    'C':    {'edge':{'F':2},                # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Cまでの最小コスト
    'D':    {'edge':{'E':3},                # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Dまでの最小コスト
    'E':    {'edge':{'Goal':2},             # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Eまでの最小コスト
    'F':    {'edge':{'E':1, 'Goal':4},      # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')},          # 頂点Fまでの最小コスト
    'Goal': {'edge':{},                     # 隣の頂点までのコスト（頂点名:コスト）
             'cost':float('inf')}           # 頂点Goalまでの最小コスト
}
#----------------------------
import heapq

q = []
heapq.heappush(q, (0, 'Start')) # スタート位置である頂点の(コスト,頂点名)をヒープキューに追加

# ダイクストラ法（最もコストの小さい頂点を順番に確認していく方法）
while len(q):       # キューがある限り実行
    # 最もコストが小さい頂点名をヒープキューから取得
    min_node_name = heapq.heappop(q)[1] # コストと頂点名が返ってくるので、頂点名だけ取得
    if min_node_name == 'Goal':         # ゴール位置の頂点だった場合
        print('解：最小コストは', nodes['Goal']['cost'])    # 最小コストを表示して終了
        break
    # 最もコストが小さい頂点からの辺を繰り返しチェックする
    for dst, cost in nodes[min_node_name]['edge'].items():
        # 次の頂点までのコストが更新対象であれば更新
        if nodes[dst]['cost'] > nodes[min_node_name]['cost'] + cost:
            nodes[dst]['cost'] = nodes[min_node_name]['cost'] + cost
            # コストを更新した頂点の(コスト,頂点名)をヒープキューに追加
            heapq.heappush(q, (nodes[dst]['cost'], dst))

[実行結果]

解：最小コストは 8

前回同様 頂点Start から 頂点Goal までの最小コストは 8 であることを導き出すことができました。

ヒープキュー を使うことにより、ソースコードがすっきりした感じがします。

また、最小コストの頂点取得の 検索効率があがった ので処理も高速化しているはずです。
（今回のグラフはシンプルすぎて効果を実感できないかもしれませんが・・・）