UMAPは、t-SNEと同様の精度がありながら処理速度も速く、4次元以上の圧縮に対応しているという次元削減のトレンドになりつつある手法です。
ただし、t-SNEと同じようにパラメータの調整は必要です。
非常に高次元で大量のデータについても現実的な時間で実行でき、非線形の高次元データを低次元して可視化する手法として主流になっています。
UMAPライブラリのインストール
まずはUMAPライブラリをインストールします。
[Google Colaboratory]
1
| !pip3 install umap-learn
|
[実行結果]
UMAPを実行
UMAPを実行します。(8行目)
また、比較のためにt-SNEも合わせて実行します。(4行目)
前前回読み込んだMNISTデータを使用しています。
[Google Colaboratory]
1
2
3
4
5
6
7
8
9
10
11
12
| import umap
start_time_tsne = time.time()
X_reduced = TSNE(n_components=2, random_state=0).fit_transform(digits.data)
interval_tsne = time.time() - start_time_tsne
start_time_umap = time.time()
embedding = umap.UMAP(n_components=2, random_state=0).fit_transform(digits.data)
interval_umap = time.time() - start_time_umap
print("tsne : {}s".format(np.round(interval_tsne,2)))
print("umap : {}s".format(np.round(interval_umap,2)))
|
[実行結果]

t-SNEよりも、UMAPの方が速く終了していることが確認できます。
可視化
t-SNEの結果とUMAPの結果を可視化します。
[Google Colaboratory]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| plt.figure(figsize=(10,8))
plt.subplot(2, 1, 1)
for each_label in digits.target_names:
c_plot_bool = digits.target == each_label
plt.scatter(X_reduced[c_plot_bool, 0], X_reduced[c_plot_bool, 1], label="{}".format(each_label))
plt.legend(loc="upper right")
plt.xlabel("tsne-1")
plt.ylabel("tsne-2")
plt.subplot(2, 1, 2)
for each_label in digits.target_names:
c_plot_bool = digits.target == each_label
plt.scatter(embedding[c_plot_bool, 0], embedding[c_plot_bool, 1], label="{}".format(each_label))
plt.legend(loc="upper right")
plt.xlabel("umap-1")
plt.ylabel("umap-2")
plt.show()
|
[実行結果]
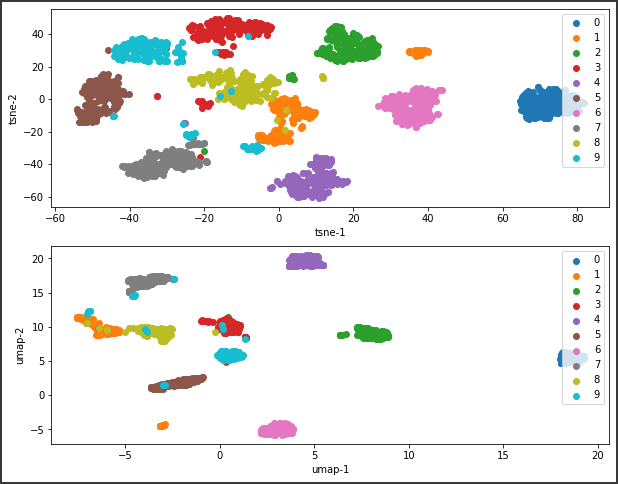
上図のt-SNEと比較して、下図のUMAPの方がそれぞれのグループがきれいに小さくまとまっていて、明確に分類されています。
つまり、より適切に情報を落とさず次元削減できているということになります。
UMAPは、どんなデータにも適用でき複雑なデータの関連性が視覚的に分かりやすくなるので、非常に有効な手法です。
次元削減アルゴリズムの選び方
次元削減をする際のアルゴリズムの選び方としては、まずPCAとUMAPの2つを試してみてより分類結果が確認しやすい方を選択するのがよいでしょう。
その2つの分類結果がいまいちであれば、t-SNEなど他のアルゴリズムを検討してみましょう。


