前回まで実行していたPCAは、データが多次元正規分布に従うことを仮定しているため、非線形データに対してはうまく動作しないという問題があります。
この問題に対処するため、非線形データの変換を行う手法がいくつかあります。
今回はその中でIsomap(Isometric mapping)を試してみます。
Isomapは多様体上の距離を測定し、多次元尺度構成法で表現する手法です。
多次元尺度構成法は近いもの同士は近くに配置し、遠いものは遠くに配置する手法で、Isomapは近いもの同士をより考慮した手法になります。
ムーンデータの取得
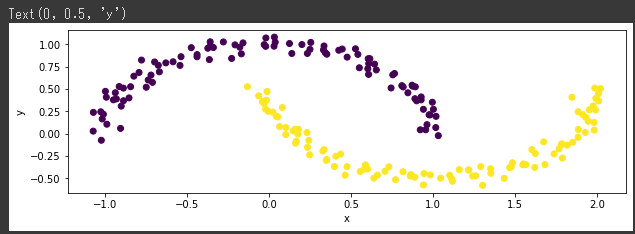
まずは非線形データとして、ムーンデータを取得します。
[Google Colaboratory]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing, decomposition, manifold
from sklearn import datasets
from sklearn.decomposition import PCA
X,Y = datasets.make_moons(n_samples=200, noise=0.05, random_state=0)
sc=preprocessing.StandardScaler()
sc.fit(X)
X_norm=sc.transform(X)
plt.figure(figsize=(10,3))
plt.scatter(X[:,0],X[:,1], c=Y)
plt.xlabel("x")
plt.ylabel("y")
|
[実行結果]
Isomap実行
取得したムーンデータに対してIsomapを実行します。(4~8行目)
比較のためPCAも実行しています。(1~2行目)
[Google Colaboratory]
1
2
3
4
5
6
7
8
| pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X_norm)
isomap_5 = manifold.Isomap(n_neighbors=5, n_components=2)
X_isomap_5 = isomap_5.fit_transform(X_norm)
isomap_10 = manifold.Isomap(n_neighbors=10, n_components=2)
X_isomap_10 = isomap_10.fit_transform(X_norm)
|
Isomapは全てのサンプル間の距離を計算しますが、細かく計算するのはサンプルごとに最も近いN個のサンプル間の距離だけです。
可視化した結果が良くない場合は、Nを変更して再び試行することになります。
このNに対応するのがn_neighborsパラメータになります。
4行目ではn_neighborsを5に、7行目ではn_neighborsを10に設定しています。(上記のソースコード)
Isomap実行結果の可視化
順番に、PCAの結果、Isomapでn_neighborsが5の結果、Isomapでn_neighborsが10の結果を可視化します。
[Google Colaboratory]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| plt.figure(figsize=(10,6))
plt.subplot(3, 1, 1)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=Y)
plt.xlabel("pca-1")
plt.ylabel("pca-2")
plt.subplot(3, 1, 2)
plt.scatter(X_isomap_5[:,0],X_isomap_5[:,1], c=Y)
plt.xlabel("isomap_n5-1")
plt.ylabel("isomap_n5-2")
plt.subplot(3, 1, 3)
plt.scatter(X_isomap_10[:,0],X_isomap_10[:,1], c=Y)
plt.xlabel("isomap_n10-1")
plt.ylabel("isomap_n10-2")
plt.show
|
[実行結果]
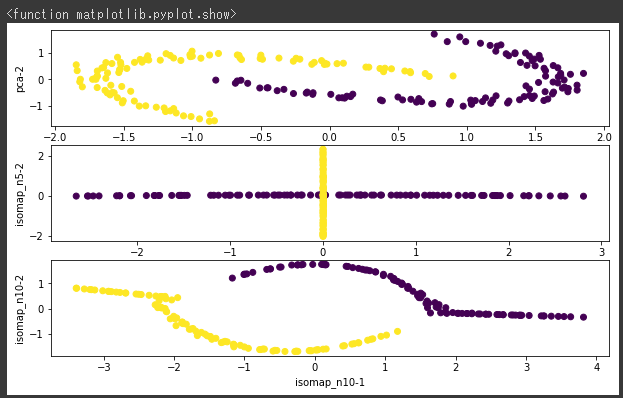
一番下のIsomapでn_neighborsが10の結果が、一番きれいに分かれていて新たな軸が作成されていることが確認できました。

