Python × AI - 寄与率(次元削減数を探索)

寄与率(explained_variance_ratio_)をもとに有効なPC数を探索します。

（前回記事で取得したワインデータと主成分分析結果を使います。）

寄与率を確認

寄与率は、主成分がどの程度、元データの情報を保持しているかを表します。

各固有値を固有値で割ったものが寄与率になります。

固有値と同じくPC1がもっとも大きく、次第に小さくなります。

寄与率を表示するソースコードは下記のようになります。

[Google Colaboratory]

1
pd.DataFrame(np.round(pca.explained_variance_ratio_,2), index=["PC{}".format(x + 1) for x in range(len(df_pca.columns))], columns=["寄与率"])

[実行結果]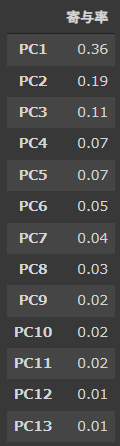

PC1が36%、PC2が19%となっておりこの２つを合わせた寄与率は55%で、PC1とPC2だけで半分以上説明できるということになります。

累積寄与率を可視化

縦軸が累積寄与率で、横軸がPCのグラフを表示します。(4行目)

また累積寄与率が90%になるまでの主成分を判断するために、90%の基準線も表示します。(2,8行目)

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
import matplotlib.ticker as ticker
line = np.full(14, 0.9)
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("PC")
plt.ylabel("cumulative contribution rate")
plt.yticks( np.arange(0, 1.1, 0.1))
plt.plot(line, "s-") 
plt.grid()
plt.show()

[実行結果]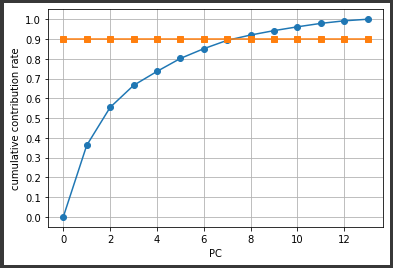

PC8のところで90%の基準線を超えていますので、PC8までを有効な次元数だと判断することができます。

より次元を削減したい場合は70%を基準することもあり、その場合はPC4までが有効な次元数となります。

累積寄与率の指定

PCAのパラメータであるn_componentsに0～1を指定すると累積寄与率が設定でき、指定した累積寄与率を超過するまでの主成分を返してくれます。

n_componentsに0.9(90%)を指定して実行します。(5行目)

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
sc = preprocessing.StandardScaler()
X = df_wine.iloc[:, 1:]
X_norm=sc.fit_transform(X)
 
pca = PCA(n_components=0.9, random_state=0)
X_pc = pca.fit_transform(X_norm)
df_pca = pd.DataFrame(X_pc, columns=["PC{}".format(i + 1) for i in range(len(X_pc[0]))])
print("主成分の数: ", pca.n_components_) 
print("保たれている情報: ", round(np.sum(pca.explained_variance_ratio_),2))
display(df_pca.head())

[実行結果]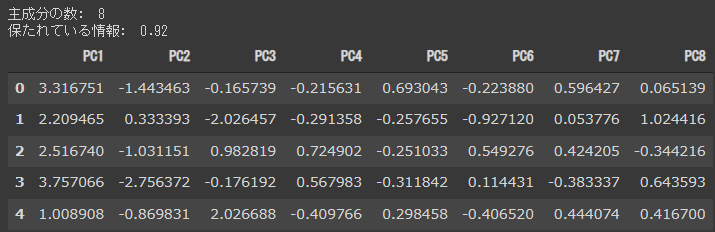

累積寄与率が90%を超過するPC8までが結果として表示されました。

累積寄与率は92%となっています。

寄与率をあらかじめ決めている場合や、大まかに有効な次元数を確認したい場合は便利な手法となります。

PCAのデータ標準化

PCAにおいてデータの標準化は基本的に実施することが推奨されていますが、ノイズデータが多い場合正しく軸をとれないことがあります。

そのため、標準化するパターンと標準化しないパターンの両方を実施して結果の良い方を使用するこをお勧めします。