Python × AI - スクリープロット(次元削減数を探索)

PCAは、教師あり学習の説明変数としての用途もあります。

その際には、次元を減らしつつも元の情報をなるべく保持しているPCまで使う必要があります。

今回は、有効なPC数を探索していきます。

ワインデータの取得

アイリスデータより次元数の多いワインデータを使用します。

ワインデータは列名が入っていないので、列名を定義しています。（2行目）

[Google Colaboratory]

1
2
3
4
df_wine=pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data", header=None)
df_wine.columns = ["class", "Alcohol", "Malic acid", "Ash", "Alcalinity of ash","Magnesium", "Total phenols", "Flavanoids", "Nonflavanoid phenols","Proanthocyanins", "Color intensity", "Hue","OD280/OD315 of diluted wines", "Proline"]
display(df_wine.shape)
display(df_wine.head())

[実行結果]

正解データが入っているため、14次元でサンプル数が178件のデータになります。

ワインデータの可視化

取得したワインデータを散布図行列で可視化します。

[Google Colaboratory]

1
2
3
from pandas import plotting
plotting.scatter_matrix(df_wine.iloc[:, 1:], figsize=(8, 8), c=list(df_wine.iloc[:, 0]), alpha=0.5)
plt.show()

[実行結果]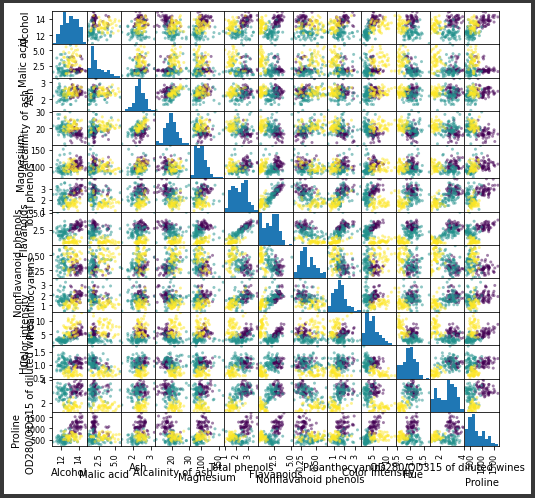

次元数が多いため、とても判断が難しくなっています。

だいたい３～４種類に分かれているような気がしなくもありません。

PCA

PCAを実行します。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.decomposition import PCA
from sklearn import preprocessing
import numpy as np
sc=preprocessing.StandardScaler()
X = df_wine.iloc[:, 1:]
X_norm=sc.fit_transform(X)
 
pca = PCA(random_state=0)
X_pc = pca.fit_transform(X_norm)
df_pca = pd.DataFrame(X_pc, columns=["PC{}".format(i + 1) for i in range(len(X_pc[0]))])
print("主成分の数: ", pca.n_components_)
print("保たれている情報: ", round(np.sum(pca.explained_variance_ratio_),2))
display(df_pca.head())

[実行結果]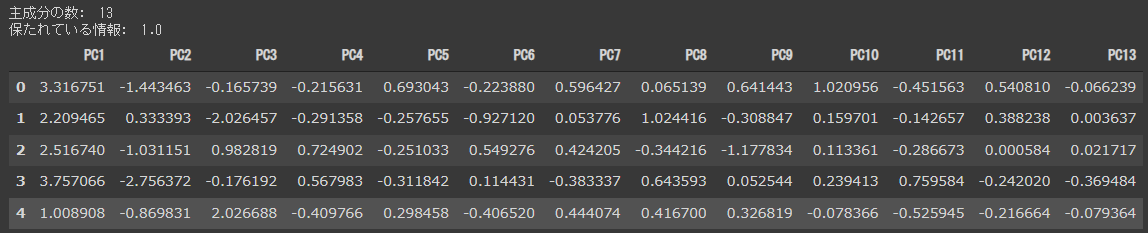

主成分の数がPC1からPC13の13個あります。

パラメータのn_componentsを指定しない場合、主成分は元データの次元数と一致します。

全次元を対象にしたので保たれている情報は1.0(100%)になります。

固有値

固有値を確認して、PC1からどこまでが有効な主成分かを探索してみましょう。

[Google Colaboratory]

1
pd.DataFrame(np.round(pca.explained_variance_, 2), index=["PC{}".format(x + 1) for x in range(len(df_pca.columns))], columns=["固有値"])

[実行結果]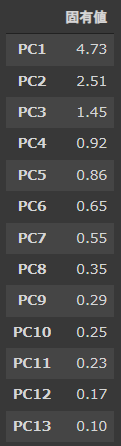

固有値(explained_variance)は、主成分の分散のことで主成分の情報量の大きさを表します。

PC1がもっとも大きく、次第に小さくなっていきます。

標準化している場合には、固有値が1.0以上のものを使うというのがもっともシンプルな判断基準となります。

今回の結果ですと、PC3までを使うことになります。

スクリープロットで可視化

次にスクリープロットを確認します。

スクリープロットは、固有値を最大から最小まで降順でプロットしたグラフのことで、崖（スクリー：scree）のような形になります。

固有値からスクリープロットを作成（2行目）し、グラフ表示するソースは以下の通りです。

固有値1.0の基準線も合わせて表示しています。（1,3行目）

[Google Colaboratory]

1
2
3
4
5
6
7
8
line = np.ones(14)
plt.plot(np.append(np.nan, pca.explained_variance_), "s-")
plt.plot(line, "s-")
plt.xlabel("PC")
plt.ylabel("explained_variance")
plt.xticks( np.arange(1, 14, 1))
plt.grid()
plt.show()

[実行結果]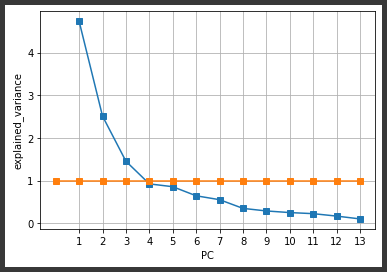

固有値が、ある段階から急に小さな値となって以降は安定する箇所までを利用することが望ましいとされています。

上記のグラフだとPC7あたりかと思いますが、使用用途に応じて±２程度で調整する必要があります。