Python × AI - 主成分と元データの相関(PCA)

前回作成した主成分を解析します。

PCAの結果

PCAの結果から取得できる値は次の通りです。

  • 固有ベクトル : components_
    PCAでデータのばらつきが大きい方向に軸を取り直した結果のベクトル。
    各主成分と元データとの相関関係（-1～1）を意味し、元のデータと主成分の影響度合いを表す。
  • 主成分得点 : explained_variance
    固有ベクトルと元データをかけ合わせた値。
    　主成分得点 ＝ 元データ × 固有ベクトル
  • 固有値 : explained_variance_
    固有ベクトルの方向に沿ったデータの分散の大きさ。
    固有値が大きい固有ベクトルほど、データの分散をよく説明しており、データの重要な特徴を捉えている。
    データを標準化している場合、各PCは1以上あれば元データより情報をもっていることになり、４次元データであれば全ての合計は4になる。
  • 寄与率 : explained_variance_ratio_
    固有値から算出した、データ特徴の捉え度合い。
    　寄与率 ＝ 固有値 ÷ 固有値の合計

相関図

元データとの関係を固有ベクトル（components）から確認します。

固有ベクトルのヒートマップを表示します。（4～12行目）

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
import seaborn as sns
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
sns.heatmap(pca.components_,
           cmap="Blues",
           annot=True,
           annot_kws={"size": 14},
           fmt=".2f",
           xticklabels=["SepalLength", "SepalWidth", "PetalLength", "PetalLength"],
           yticklabels=["PC1", "PC2", "PC3", "PC4"],
           ax=ax)
plt.show()

[実行結果]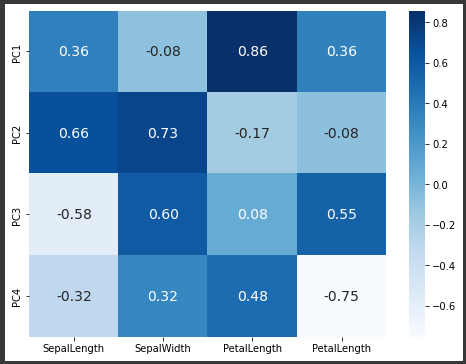

上図は、各主成分（縦軸）と元データ（横軸）との相関関係を表しています。

PC1をみると、SepalLength、PetalLength、PetalWidthの３つが平均として大きな値となっています。

PC2については、SepalWidthが強く影響しています。

このように主成分がどんな内容の軸になったのかは、PCAの結果を見て判断する必要があります。