Python × AI - 主成分分析(PCA)

主成分分析(PCA:Principal Component Analysis)は、多次元データのもつ情報をできるだけ損なわずに低次元とする方法です。

次元削減で最も簡単な方法であり、広い分野で使われています。

アイリスデータの読み込み

まずアイリスデータを読み込みます。

結果の確認用にtarget_nameに正解の花の名称を追加しています。（5～8行目）

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
df=pd.DataFrame(iris.data, columns=iris.feature_names)
df["target"] = iris.target
df.loc[df["target"]==0, "target_name"] = "setosa"
df.loc[df["target"]==1, "target_name"] = "versicolor"
df.loc[df["target"]==2, "target_name"] = "virginica"
df.head()

[実行結果]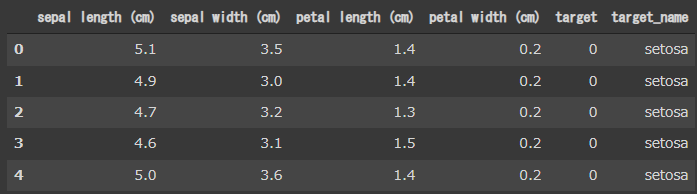

アイリスデータの散布図行列

読み込んだアイリスデータを散布図行列で可視化します。

hueパラメータに名称”target_name”を設定することで色をつけています。（2行目）

[Google Colaboratory]

1
2
import seaborn as sns
sns.pairplot(df, vars=df.columns[:4], hue="target_name")

[実行結果]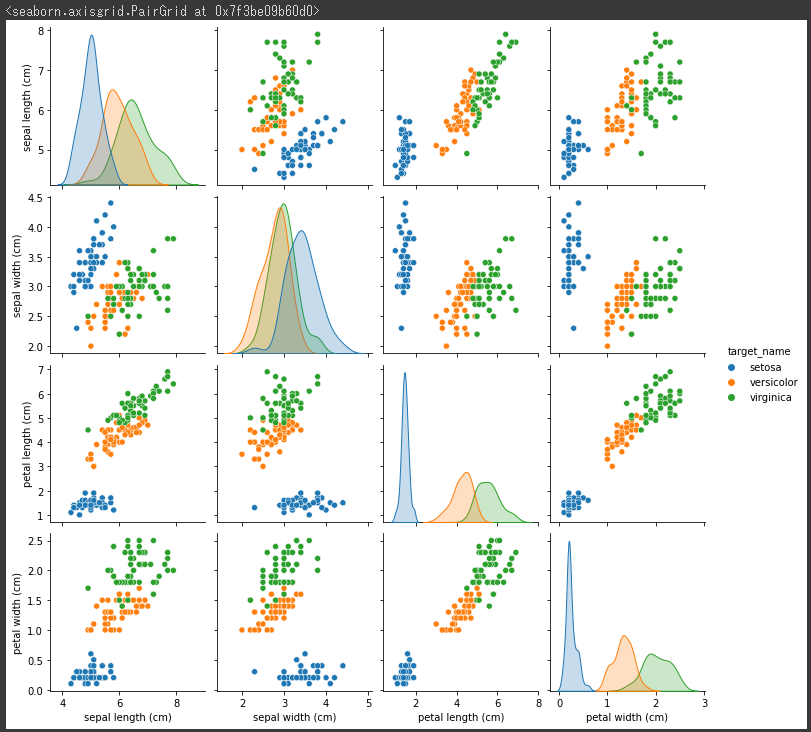

品種ごとに色分けされていて分類されていることは把握できますが、次元が多いため解釈するのが大変です。

アイリスの３次元立体図

花の品種ごとにpetal_width以外の情報を取得します。（5～6行目）

その後、３次元での可視化を行います。（7～12行目）

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(1, 1, 1, projection="3d")
for c in df["target_name"].unique():
    ax.scatter(df.iloc[:, 0][df["target_name"]==c], df.iloc[:, 1][df["target_name"]==c] , df.iloc[:, 2][df["target_name"]==c], label=c)
ax.set_title("iris 3D") 
ax.set_xlabel("sepal_length") 
ax.set_ylabel("sepal_width")  
ax.set_zlabel("petal_length") 
ax.legend(loc=2, title="legend", shadow=True)  
plt.show()

[実行結果]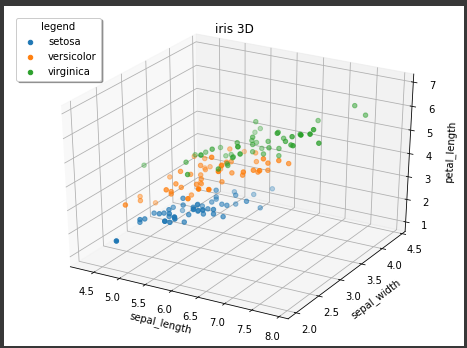

３品種に分かれているように見えますが、petal_widthの情報は全く無視してしまっています。

この情報が特徴量のある重要なデータだったという可能性もあります。

PCAを使用すれば、この４次元データを２次元データで表現することが可能になります。

PCA実行

PCAを実行し（3～4行目）、結果である主成分得点を表示します（5～8行目）。

[Google Colaboratory]

1
2
3
4
5
6
7
8
from sklearn.decomposition import PCA
import numpy as np
pca = PCA(random_state=0)
X_pc = pca.fit_transform(df.iloc[:, 0:4])
df_pca = pd.DataFrame(X_pc, columns=["PC{}".format(i + 1) for i in range(len(X_pc[0]))])
print("主成分の数: ", pca.n_components_) 
print("保たれている情報: ", np.sum(pca.explained_variance_ratio_))
display(df_pca.head())

[実行結果]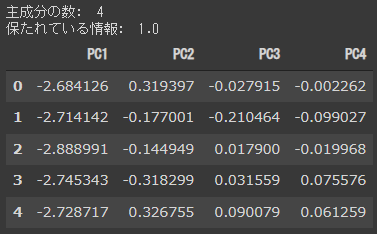

横軸が主成分(PC:Principal Component)で、縦軸が各サンプルを表します。

主成分(PC)とは、データを要約（縮小）したあとの新しい合成変数で、第１主成分(PC1)に最も多くの情報が集まっていて第２主成分(PC2)以降にだんだんと情報が小さくなります。

PC1とPC2を可視化

多くの情報が集まっているPC1とPC2を可視化します。

[Google Colaboratory]

1
sns.scatterplot(x="PC1", y="PC2", data=df_pca, hue=df["target_name"])

[実行結果]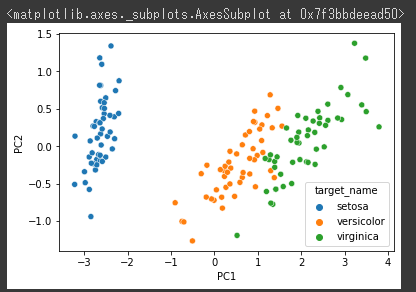

４次元あったデータを２次元で可視化することができました。

うまく３種類に分類されています。

PCAの用途はいくつかあるのですが、多次元データの特徴を低次元に次元削減し可視化する手段としてとても有効です。