価値の定義と算出 Bellman Equation

価値を再帰的かつ期待値で表現する手法をBellman Equationと呼びます。（Valueベース）
Bellman Equationを使えば各状態の価値が計算可能となります。

まず価値を返す関数を定義します。

def V(s, gamma=0.99):
    V = R(s) + gamma * max_V_on_next_state(s)
    return V

報酬関数を定義します。
エピソード終了のとき”happy_end”であれば1を返し、”bad_end”であれば-1を返します。
エピソードが終了していなければ0を返します。

def R(s):
    if s == "happy_end":
        return 1
    elif s == "bad_end":
        return -1
    else:
        return 0

全ての行動でV(s)を計算し値が最大になる価値を返します。
評価vの計算式は確率遷移×遷移先の価値となります。

upかdownかを繰り返していき5回行動したら終了となります。

def max_V_on_next_state(s):
    # If game end, expected value is 0.
    if s in ["happy_end", "bad_end"]:
        return 0

    actions = ["up", "down"]
    values = []
    for a in actions:
        transition_probs = transit_func(s, a)
        v = 0
        for next_state in transition_probs:
            prob = transition_probs[next_state]    # 確率遷移
            v += prob * V(next_state)              # 遷移先の価値
        values.append(v)
    return max(values)

遷移関数を定義します。

• 引数sには”state”や”state_up_up”、”state_down_down”などが受け渡されます。
• 引数aは”up”か”down”が設定されます。
• エピソード完了時は1要素が返り、途中の場合は2要素が返ります。

def transit_func(s, a):
    actions = s.split("_")[1:]
    LIMIT_GAME_COUNT = 5
    HAPPY_END_BORDER = 4
    MOVE_PROB = 0.9

    def next_state(state, action):
        return "_".join([state, action])

    if len(actions) == LIMIT_GAME_COUNT:
        # 最大行動数と一致するのでエピソード終了
        up_count = sum([1 if a == "up" else 0 for a in actions])
        state = "happy_end" if up_count >= HAPPY_END_BORDER else "bad_end"
        prob = 1.0
        return {state: prob}
    else:
        opposite = "up" if a == "down" else "down"
        return {
            next_state(s, a): MOVE_PROB,
            next_state(s, opposite): 1 - MOVE_PROB
        }

実際に価値V(s)の計算を行ってみます。

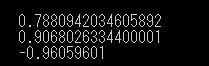
if __name__ == "__main__":
    print(V("state"))
    print(V("state_up_up"))
    print(V("state_down_down"))

upの数が多い方が評価されます。

参考

Pythonで学ぶ強化学習 -入門から実践まで- サンプルコード

Contents

None