迷路をSarsaで解く

価値反復法の１つSarsaで迷路を攻略します。
Sarsaでは1エピソードごとではなく1ステップごとに更新を行います。

まず使用するパッケージをインポートします。

1
2
3
4
# 使用するパッケージの宣言
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

次に迷路の初期状態を描画します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 初期位置での迷路の様子

# 図を描く大きさと、図の変数名を宣言
fig = plt.figure(figsize=(5, 5))
ax = plt.gca()

# 赤い壁を描く
plt.plot([1, 1], [0, 1], color='red', linewidth=2)
plt.plot([1, 2], [2, 2], color='red', linewidth=2)
plt.plot([2, 2], [2, 1], color='red', linewidth=2)
plt.plot([2, 3], [1, 1], color='red', linewidth=2)

# 状態を示す文字S0～S8を描く
plt.text(0.5, 2.5, 'S0', size=14, ha='center')
plt.text(1.5, 2.5, 'S1', size=14, ha='center')
plt.text(2.5, 2.5, 'S2', size=14, ha='center')
plt.text(0.5, 1.5, 'S3', size=14, ha='center')
plt.text(1.5, 1.5, 'S4', size=14, ha='center')
plt.text(2.5, 1.5, 'S5', size=14, ha='center')
plt.text(0.5, 0.5, 'S6', size=14, ha='center')
plt.text(1.5, 0.5, 'S7', size=14, ha='center')
plt.text(2.5, 0.5, 'S8', size=14, ha='center')
plt.text(0.5, 2.3, 'START', ha='center')
plt.text(2.5, 0.3, 'GOAL', ha='center')

# 描画範囲の設定と目盛りを消す設定
ax.set_xlim(0, 3)
ax.set_ylim(0, 3)
plt.tick_params(axis='both', which='both', bottom='off', top='off',
                labelbottom='off', right='off', left='off', labelleft='off')

# 現在地S0に緑丸を描画する
line, = ax.plot([0.5], [2.5], marker="o", color='g', markersize=60)

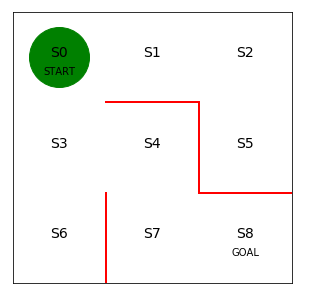
実行結果1

初期の方策を決定するパラメータtheta_0を設定します。

行は状態0～7を表し、列は上、右、下、左へ行動できるかどうかを表します。
状態8はゴールなので方策の定義は不要です。

1
2
3
4
5
6
7
8
9
10
11
# 初期の方策を決定するパラメータtheta_0を設定
# 行は状態0～7、列は移動方向で↑、→、↓、←を表す
theta_0 = np.array([[np.nan, 1, 1, np.nan],  # s0
                    [np.nan, 1, np.nan, 1],  # s1
                    [np.nan, np.nan, 1, 1],  # s2
                    [1, 1, 1, np.nan],       # s3
                    [np.nan, np.nan, 1, 1],  # s4
                    [1, np.nan, np.nan, np.nan],  # s5
                    [1, np.nan, np.nan, np.nan],  # s6
                    [1, 1, np.nan, np.nan],  # s7、※s8はゴールなので、方策はなし
                    ])

方策パラメータθ0をランダム方策piに変換する関数を定義します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 方策パラメータtheta_0をランダム方策piに変換する関数の定義
def simple_convert_into_pi_from_theta(theta):
    '''単純に割合を計算する'''
    [m, n] = theta.shape  # thetaの行列サイズを取得
    pi = np.zeros((m, n))
    for i in range(0, m):
        pi[i, :] = theta[i, :] / np.nansum(theta[i, :])  # 割合の計算

    pi = np.nan_to_num(pi)  # nanを0に変換

    return pi

# ランダム行動方策pi_0を求める
pi_0 = simple_convert_into_pi_from_theta(theta_0)

初期の行動価値関数Qを設定します。

行動価値関数は、行が状態sを表し、列が行動aを表します。
最初は正しい行動価値がわからないのでランダムな値を設定します。

1
2
3
4
# 初期の行動価値関数Qを設定
[a, b] = theta_0.shape  # 行と列の数をa, bに格納
Q = np.random.rand(a, b) * theta_0
# * theta0をすることで要素ごとに掛け算をし、Qの壁方向の値がnanになる

ε-greedy法を実装します。
一定確率εでランダムに行動し、残りの1-εの確率で行動価値Qが最大になる行動をとります。

get_action()が行動を求める関数で、get_s_next()が行動を引数に次の状態を求める関数になります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# ε-greedy法を実装
def get_action(s, Q, epsilon, pi_0):
    direction = ["up", "right", "down", "left"]

    # 行動を決める
    if np.random.rand() < epsilon:
        # εの確率でランダムに動く
        next_direction = np.random.choice(direction, p=pi_0[s, :])
    else:
        # Qの最大値の行動を採用する
        next_direction = direction[np.nanargmax(Q[s, :])]

    # 行動をindexに
    if next_direction == "up":
        action = 0
    elif next_direction == "right":
        action = 1
    elif next_direction == "down":
        action = 2
    elif next_direction == "left":
        action = 3

    return action

def get_s_next(s, a, Q, epsilon, pi_0):
    direction = ["up", "right", "down", "left"]
    next_direction = direction[a]  # 行動aの方向

    # 行動から次の状態を決める
    if next_direction == "up":
        s_next = s - 3  # 上に移動するときは状態の数字が3小さくなる
    elif next_direction == "right":
        s_next = s + 1  # 右に移動するときは状態の数字が1大きくなる
    elif next_direction == "down":
        s_next = s + 3  # 下に移動するときは状態の数字が3大きくなる
    elif next_direction == "left":
        s_next = s - 1  # 左に移動するときは状態の数字が1小さくなる

    return s_next

行動価値関数Q(s,a)が正しい値になるように学習して更新する処理を実装します。
gammaは時間割引率で未来の報酬を割り引いています。

1
2
3
4
5
6
7
8
# Sarsaによる行動価値関数Qの更新
def Sarsa(s, a, r, s_next, a_next, Q, eta, gamma):
    if s_next == 8:  # ゴールした場合
        Q[s, a] = Q[s, a] + eta * (r - Q[s, a])
    else:
        Q[s, a] = Q[s, a] + eta * (r + gamma * Q[s_next, a_next] - Q[s, a])

    return Q

Sarsaに従って迷路を解く処理を実装します。
1エピソードごとではなく1ステップごとに更新を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Sarsaで迷路を解く関数の定義、状態と行動の履歴および更新したQを出力
def goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi):
    s = 0  # スタート地点
    a = a_next = get_action(s, Q, epsilon, pi)  # 初期の行動
    s_a_history = [[0, np.nan]]  # エージェントの移動を記録するリスト

    while (1):  # ゴールするまでループ
        a = a_next  # 行動更新

        s_a_history[-1][1] = a
        # 現在の状態（つまり一番最後なのでindex=-1）に行動を代入

        s_next = get_s_next(s, a, Q, epsilon, pi)
        # 次の状態を格納

        s_a_history.append([s_next, np.nan])
        # 次の状態を代入。行動はまだ分からないのでnanにしておく

        # 報酬を与え,　次の行動を求めます
        if s_next == 8:
            r = 1  # ゴールにたどり着いたなら報酬を与える
            a_next = np.nan
        else:
            r = 0
            a_next = get_action(s_next, Q, epsilon, pi)
            # 次の行動a_nextを求めます。

        # 価値関数を更新
        Q = Sarsa(s, a, r, s_next, a_next, Q, eta, gamma)

        # 終了判定
        if s_next == 8:  # ゴール地点なら終了
            break
        else:
            s = s_next

    return [s_a_history, Q]

価値関数の更新を繰り返す処理を実装します。
今回の学習終了条件は、100エピソードを行うこととしました。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Sarsaで迷路を解く
eta = 0.1      # 学習率
gamma = 0.9    # 時間割引率
epsilon = 0.5  # ε-greedy法の初期値
v = np.nanmax(Q, axis=1)  # 状態ごとに価値の最大値を求める
is_continue = True
episode = 1

while is_continue:  # is_continueがFalseになるまで繰り返す
    print("エピソード:" + str(episode))

    # ε-greedyの値を少しずつ小さくする
    epsilon = epsilon / 2

    # Sarsaで迷路を解き、移動した履歴と更新したQを求める
    [s_a_history, Q] = goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi_0)

    # 状態価値の変化
    new_v = np.nanmax(Q, axis=1)  # 状態ごとに価値の最大値を求める
    print(np.sum(np.abs(new_v - v)))  # 状態価値の変化を出力
    v = new_v

    print("迷路を解くのにかかったステップ数は" + str(len(s_a_history) - 1) + "です")

    # 100エピソード繰り返す
    episode = episode + 1
    if episode > 100:
        break

実行結果 エピソード:1～8
エピソード2ですでに最小ステップ4となっています。エピソード3では6ステップと増えましたがその後は、ずっと4ステップのままです。

実行結果 エピソード:92～100

エピソード100を実行するまでもなくずっと最小の4ステップで安定しました。
今回の迷路と解く問題では方策反復法よりも価値反復法の方が早く学習できるという結果になりました。

(Google Colaboratoryで動作確認しています。)

参考

つくりながら学ぶ！深層強化学習 サポートページ