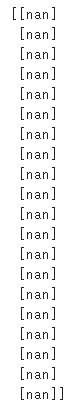ニューラルネットワークで回帰分析

ニューラルネットワークで回帰分析をします。
まずは必要なモジュールのインポートと共通関数の定義をします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt

import chainer.optimizers as Opt
import chainer.functions as F
import chainer.links as L
from chainer import Variable, Chain, config, cuda

# -------------- #
# 共通関数の定義 #
# -------------- #
# データ振り分け関数
def data_divide(Dtrain, D, xdata, tdata):
    index = np.random.permutation(range(D))
    xtrain = xdata[index[0:Dtrain],:]
    ttrain = tdata[index[0:Dtrain]]
    xtest = xdata[index[Dtrain:D],:]
    ttest = tdata[index[Dtrain:D]]
    return xtrain, xtest, ttrain, ttest

# グラフ表示関数
def show_graph(result1, result2, title, xlabel, ylabel, ymin=0.0, ymax=1.0):
    # 学習記録の表示(誤差)
    Tall = len(result1)
    plt.figure(figsize=(8, 6))
    plt.plot(range(Tall), result1, label='train')
    plt.plot(range(Tall), result2, label='test')
    plt.title(title)
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.xlim([0, Tall])
    plt.ylim(ymin, ymax)
    plt.legend()
    plt.show()

# 回帰関数の定義
def learning_regression(model, optNN, data, T=10):
    train_loss = []
    test_loss = []
    for time in range(T):
        config.train = True
        optNN.target.cleargrads()  # zerogradsより記憶容量の確保にいい
        ytrain = model(data[0])
        loss_train = F.mean_squared_error(ytrain, data[2])
        loss_train.backward()
        optNN.update()
        
        config.train = False
        ytest = model(data[1])
        loss_test = F.mean_squared_error(ytest, data[3])
        
        train_loss.append(loss_train.data)
        test_loss.append(loss_test.data)
    return train_loss, test_loss

データを準備します。
x軸を-5から5までの等間隔100個分準備し、その後適当な関数でy軸に変換します。

1
2
3
4
5
6
7
8
# 等間隔の数値を用意する(x軸用)
D = 100
ndata = np.linspace(-5.0, 5.0, D)

# 関数でデータ作成
N = 1
xdata = ndata.reshape(D, N).astype(np.float32) # 2次元配列に変換(100行1列)
tdata = (np.sin(ndata) + np.sin(2.0 * ndata)).reshape(D, N).astype(np.float32)

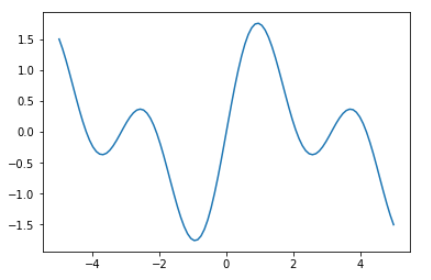
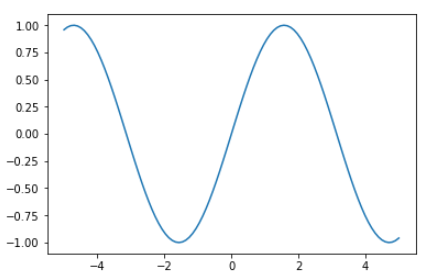
作成したデータを視覚化します。

1
2
3
# 作成したデータをグラフ表示
plt.plot(xdata, tdata)
plt.show()

結果

ニューラルネットワークを作成し関数化します。
非線形関数はreluを使用します。

1
2
3
4
5
6
7
8
9
10
11
# 回帰のニューラルネットワークを作成し、関数化
C = 1     # 出力数
H = 20    # 中間層の数
NN = Chain(l1=L.Linear(N, H), l2=L.Linear(H, C), bnorm1=L.BatchNormalization(H))

def model(x):
    h = NN.l1(x)
    h = F.relu(h)
    h = NN.bnorm1(h)
    y = NN.l2(h)
    return y

参考までに学習前のニューラルネットワークの状態を確認します。
まずは重さです。

1
2
# ニューラルネットワークの状態調査
print(NN.l1.W.data)  # 最初はでたらめな重さ

結果
初期値としてでたらめな重さが設定されています。

次に勾配を表示してみます。

1
2
# ニューラルネットワークの勾配表示
print(NN.l1.W.grad)   # 全て未計算(Not a Number)

結果
こちらはnan(Not a number)が設定されています。

最適化手法を設定し学習を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 最適化手法の設定
optNN = Opt.MomentumSGD()
optNN.setup(NN)

# 学習結果記録用
train_loss = []
test_loss = []

Dtrain = D // 2    # 訓練データ数
xtrain, xtest, ttrain, ttest = data_divide(Dtrain, D, xdata, tdata) # データ分割
data = [xtrain, xtest, ttrain, ttest]
result = [train_loss, test_loss]

train_loss, test_loss = learning_regression(model, optNN, data, 1000)

show_graph(train_loss, test_loss, 'loss function', 'step', 'loss function', 0.0, 3.0)

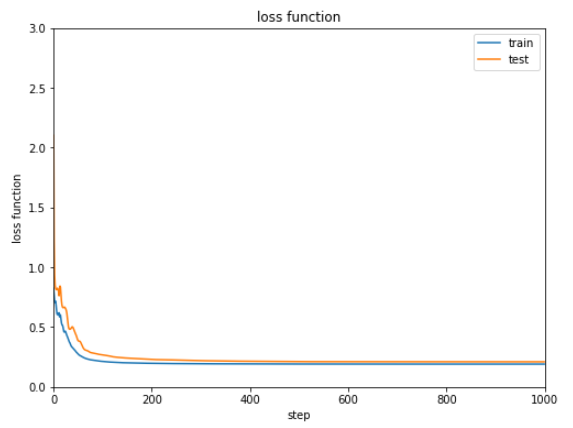
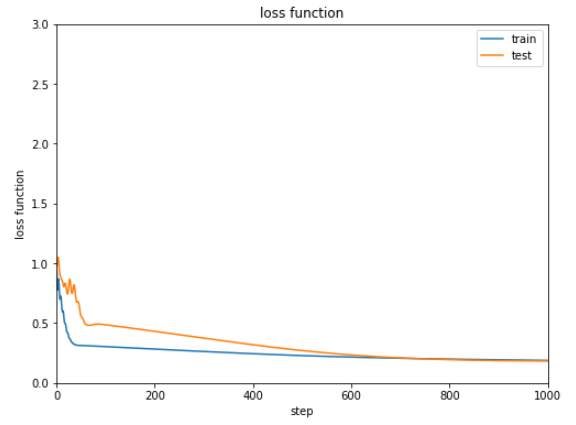
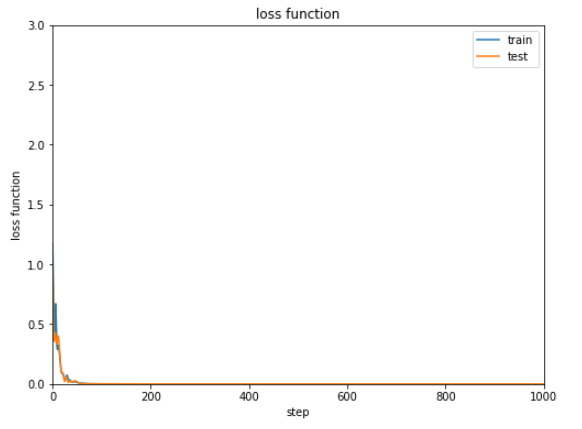
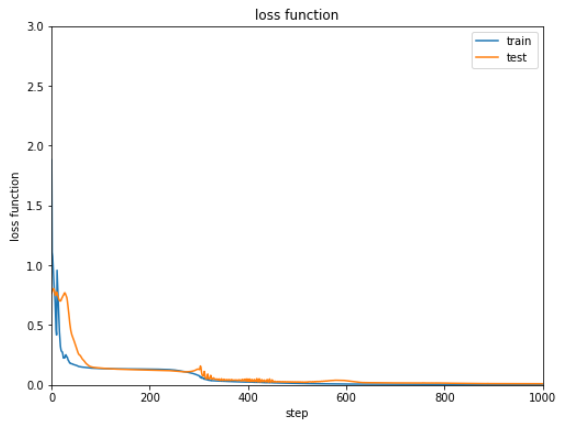
学習結果の誤差は下記のようになります。
結果

次第に減少してはいますが0.2から0.3付近で改善しなくなっています。

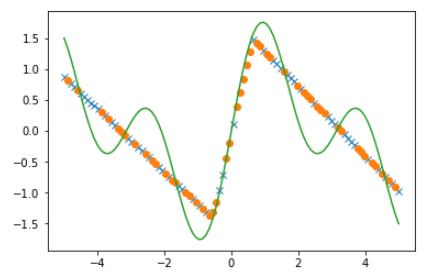
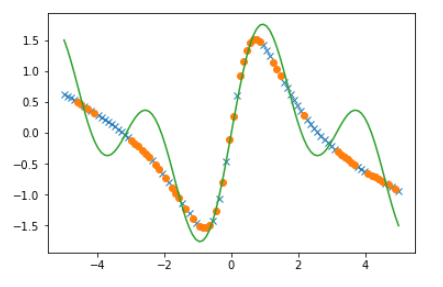
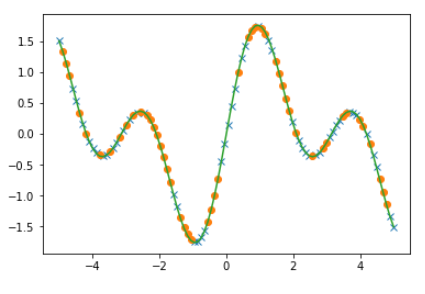
回帰の結果を比較します。

1
2
3
4
5
6
7
8
# 回帰の結果を比較する
config.train = False
ytrain = model(xtrain).data
ytest = model(xtest).data
plt.plot(xtrain, ytrain, marker='x', linestyle='None')
plt.plot(xtest, ytest, marker='o', linestyle='None')
plt.plot(xdata, tdata)
plt.show()

結果
結果はぜんぜん合っていないようです。なんらかの改善策をとる必要がありそうです。

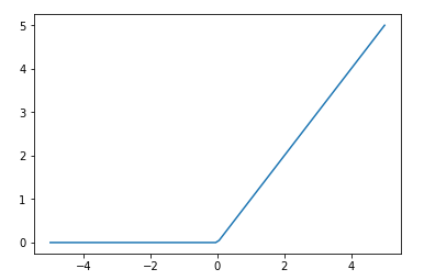
非線形関数調整してみます。
今回使ったreluの形は下記のようになっており、今回学習するデータには合わないようです。

1
2
3
4
# F.reluの形を調べる
ydata = F.relu(xdata).data
plt.plot(xdata, ydata)
plt.show()

結果

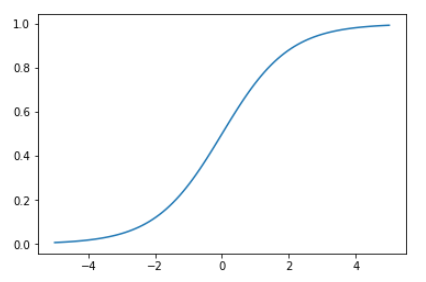
別の非線形関数sigmoidの形を調べると、reluよりは今回学習するデータに近いようにみえます。

1
2
3
4
# F.sigmoidの形を調べる
ydata = F.sigmoid(xdata).data
plt.plot(xdata, ydata)
plt.show()

結果

非線形関数をreluからsigmoidに変更し、同じように学習・結果表示を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 回帰のニューラルネットワークを作成し、関数化
C = 1     # 出力数
H = 20    # 中間層の数
NN = Chain(l1=L.Linear(N, H), l2=L.Linear(H, C), bnorm1=L.BatchNormalization(H))

def model(x):
    h = NN.l1(x)
    h = F.sigmoid(h)   # シグモイドに変更
    h = NN.bnorm1(h)
    h = NN.l2(h)
    return h

# 最適化手法の設定
optNN = Opt.MomentumSGD()
optNN.setup(NN)

# 学習結果記録用
train_loss = []
test_loss = []

Dtrain = D // 2    # 訓練データ数
xtrain, xtest, ttrain, ttest = data_divide(Dtrain, D, xdata, tdata)
data = [xtrain, xtest, ttrain, ttest]
result = [train_loss, test_loss]

train_loss, test_loss = learning_regression(model, optNN, data, 1000)

show_graph(train_loss, test_loss, 'loss function', 'step', 'loss function', 0.0, 3.0)

結果
誤差に関しては２つの非線形関数でそれほど結果が変わりませんでした。

回帰の結果を確認してみます。

1
2
3
4
5
6
7
8
# 回帰の結果を比較する
config.train = False
ytrain = model(xtrain).data
ytest = model(xtest).data
plt.plot(xtrain, ytrain, marker='x', linestyle='None')
plt.plot(xtest, ytest, marker='o', linestyle='None')
plt.plot(xdata, tdata)
plt.show()

結果
reluよりはsigmoidを使った方がだいぶましになったように思われます。

ただまだまだ納得いく結果ではありません。
ほかの非線形関数を調べたところsin関数というのがありました。

1
2
3
4
# F.sinの形を調べる
ydata = F.sin(xdata).data
plt.plot(xdata, ydata)
plt.show()

結果
この関数はかなり今回回帰分析を行いたいグラフと形が似ているようです。

非線形関数をsinに変更してまたまた回帰分析を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 回帰のニューラルネットワークを作成し、関数化
C = 1     # 出力数
H = 20    # 中間層の数
NN = Chain(l1=L.Linear(N, H), l2=L.Linear(H, C), bnorm1=L.BatchNormalization(H))

def model(x):
    h = NN.l1(x)
    h = F.sin(h)   # サインに変更
    h = NN.bnorm1(h)
    h = NN.l2(h)
    return h

# 最適化手法の設定
optNN = Opt.MomentumSGD()
optNN.setup(NN)

# 学習結果記録用
train_loss = []
test_loss = []

Dtrain = D // 2    # 訓練データ数
xtrain, xtest, ttrain, ttest = data_divide(Dtrain, D, xdata, tdata)
data = [xtrain, xtest, ttrain, ttest]
result = [train_loss, test_loss]

train_loss, test_loss = learning_regression(model, optNN, data, 1000)

show_graph(train_loss, test_loss, 'loss function', 'step', 'loss function', 0.0, 3.0)

結果
誤差は十分に下がることが確認できました。

回帰の結果も確認してみます。

1
2
3
4
5
6
7
8
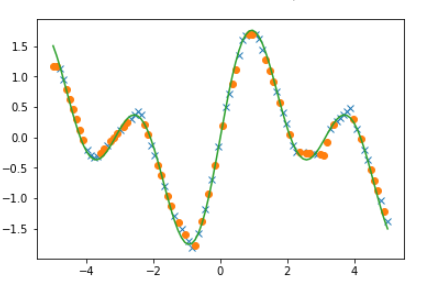
# 回帰の結果を比較する
config.train = False
ytrain = model(xtrain).data
ytest = model(xtest).data
plt.plot(xtrain, ytrain, marker='x', linestyle='None')
plt.plot(xtest, ytest, marker='o', linestyle='None')
plt.plot(xdata, tdata)
plt.show()

結果
完璧な結果がでました。
ただ今回はグラフの見た目でそれに近い非線形関数を使うという少しずるい手順を踏んでしましました。

relu関数のまま結果を改善することはできないのでしょうか。
試しにニューラルネットワークの階層を増やしてみました。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# ４層のニューラルネットワークを作成し関数化
C = 1     # 出力の種類
H1 = 5
H2 = 5
H3 = 5
layers = {}
layers['l1'] = L.Linear(N, H1)
layers['l2'] = L.Linear(H1, H2)
layers['l3'] = L.Linear(H2, H3)
layers['l4'] = L.Linear(H3, C)
layers['bnorm1'] = L.BatchNormalization(H1)
layers['bnorm2'] = L.BatchNormalization(H2)
layers['bnorm3'] = L.BatchNormalization(H3)
NN = Chain(**layers)

def model(x):
    h = NN.l1(x)
    h = F.relu(h)
    h = NN.bnorm1(h)
    h = NN.l2(h)
    h = F.relu(h)
    h = NN.bnorm2(h)
    h = NN.l3(h)
    h = F.relu(h)
    h = NN.bnorm3(h)
    y = NN.l4(h)
    return y

# 最適化手法の設定
optNN = Opt.MomentumSGD()
optNN.setup(NN)

# 学習結果記録用
train_loss = []
test_loss = []

Dtrain = D // 2    # 訓練データ数
xtrain, xtest, ttrain, ttest = data_divide(Dtrain, D, xdata, tdata)
data = [xtrain, xtest, ttrain, ttest]
result = [train_loss, test_loss]

train_loss, test_loss = learning_regression(model, optNN, data, 1000)

show_graph(train_loss, test_loss, 'loss function', 'step', 'loss function', 0.0, 3.0)

# 回帰の結果を比較する
config.train = False
ytrain = model(xtrain).data
ytest = model(xtest).data
plt.plot(xtrain, ytrain, marker='x', linestyle='None')
plt.plot(xtest, ytest, marker='o', linestyle='None')
plt.plot(xdata, tdata)
plt.show()

結果は以下の通りです。
結果
誤差は十分に下がっています。

結果
回帰の結果もなかなか良いものがでました。回帰分析の結果を改善するためには非線形関数を変更する方法とは別に、ニューラルネットワークの階層を深くするのも有効な手段だと言えそうです。

(Google Colaboratoryで動作確認しています。)