Problem Description
We will analyze the performance of three popular sorting algorithms:
- Bubble Sort (Simple but slow for large datasets),
- Merge Sort (Efficient divide-and-conquer algorithm),
- Python’s Built-in Timsort (Used by Python’s
sorted()function).
The goal is to:
- Measure the time taken by each algorithm to sort a list of random numbers of increasing size.
- Visualize the time complexity and compare their performance.
Python Solution
1 | import time |
Explanation of the Code
Sorting Algorithms:
- Bubble Sort:
Compares adjacent elements and swaps them if they are in the wrong order.
Very slow for large datasets O(n2). - Merge Sort:
Recursively divides the array into halves, sorts each half, and then merges them O(nlogn). - Timsort:
Python’s optimized built-in algorithm, designed for real-world performance O(nlogn).
- Bubble Sort:
Performance Measurement:
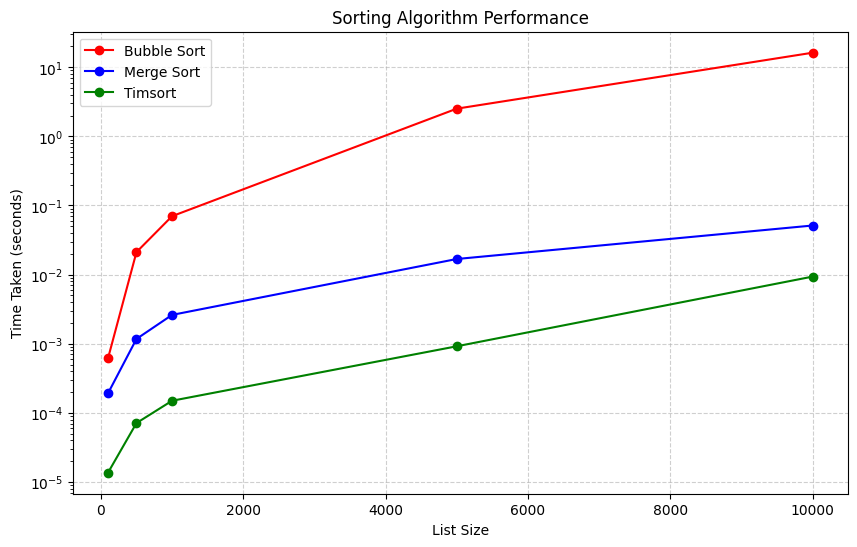
- The algorithms are tested on arrays of increasing size: 100, 500, 1000, 5000, and 10,000.
- Execution time for each algorithm is measured using Python’s
timemodule.
Visualization:
- The results are plotted with the list size on the x-axis and execution time on the y-axis.
- A logarithmic scale is used for the y-axis to highlight differences between the algorithms.
Graph Explanation
- X-axis:
Represents the size of the list. - Y-axis:
Represents the time taken (in seconds) on a logarithmic scale. - Observations:
- Bubble Sort:
The performance deteriorates rapidly as the list size increases, due to its quadratic time complexity O(n2). - Merge Sort:
Performs significantly better for large lists, maintaining O(nlogn) complexity. - Timsort:
Outperforms both Bubble Sort and Merge Sort, as it is optimized for typical sorting use cases.
- Bubble Sort:
This example illustrates how algorithmic choices impact performance and the importance of selecting efficient algorithms for large datasets.