The Halting Problem (Illustration via the Collatz Conjecture)

Problem

The Halting Problem is a famous problem in computability theory, which states that no algorithm can universally determine whether an arbitrary program will halt or run forever.

To illustrate this concept, we’ll use the Collatz Conjecture, which is a sequence defined as follows:

  1. Start with any positive integer (n).
  2. If (n) is even, divide it by 2.
  3. If (n) is odd, multiply it by 3 and add 1.
  4. Repeat until (n=1).

The conjecture states that this sequence will always reach 1, no matter the starting (n).

However, this has not been proven for all integers.

We’ll implement this in Python, simulate the process for various starting values of (n), and visualize the results.

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import matplotlib.pyplot as plt

# Function to compute the Collatz sequence
def collatz_sequence(n):
    steps = 0
    sequence = [n]
    while n != 1:
        if n % 2 == 0:
            n = n // 2
        else:
            n = 3 * n + 1
        sequence.append(n)
        steps += 1
    return sequence, steps

# Simulate Collatz for multiple starting numbers
start_numbers = range(1, 51)  # Starting numbers from 1 to 50
step_counts = []  # To store the number of steps for each starting number

# Compute the sequence for each starting number
for start in start_numbers:
    _, steps = collatz_sequence(start)
    step_counts.append(steps)

# Visualization
plt.figure(figsize=(12, 6))

# Plot the number of steps for each starting number
plt.bar(start_numbers, step_counts, color="skyblue", edgecolor="black")
plt.title("Collatz Conjecture: Number of Steps to Reach 1")
plt.xlabel("Starting Number")
plt.ylabel("Number of Steps")
plt.grid(axis="y", linestyle="--", alpha=0.7)
plt.show()

# Example sequence for a specific number
n_example = 27
sequence, _ = collatz_sequence(n_example)

# Plot the sequence for the example starting number
plt.figure(figsize=(12, 6))
plt.plot(range(len(sequence)), sequence, marker="o", color="red", label=f"Starting Number: {n_example}")
plt.title(f"Collatz Sequence for Starting Number {n_example}")
plt.xlabel("Step")
plt.ylabel("Value")
plt.grid(True, linestyle="--", alpha=0.7)
plt.legend()
plt.show()

Explanation

  1. Collatz Sequence:

    • The function collatz_sequence(n) generates the sequence for a given starting number (n) and counts the steps until it reaches 1.

  2. Simulation:

    • For each starting number from 1 to 50, the sequence is computed, and the number of steps is recorded.

  3. Visualization:

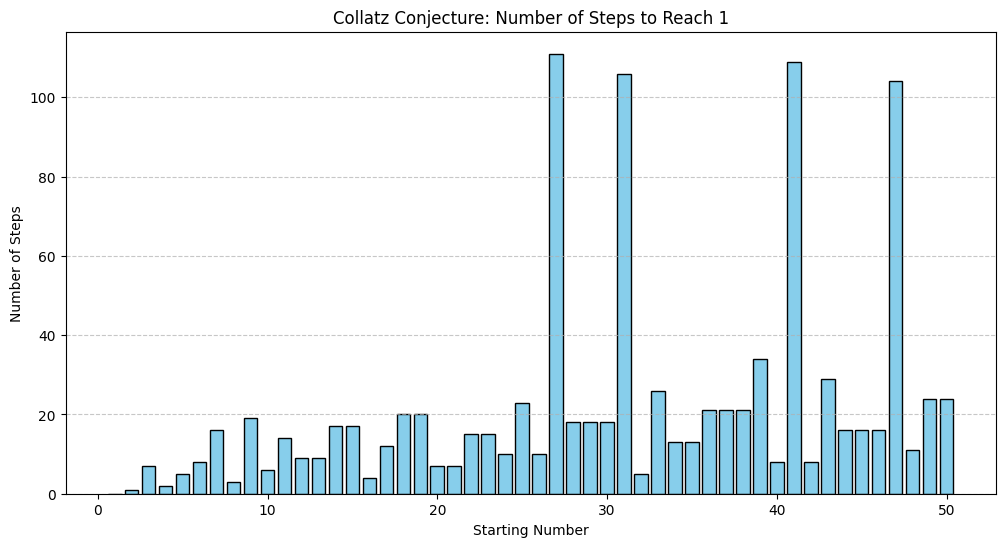
    • Steps to Reach 1:
      • A bar plot shows the number of steps needed for each starting number to reach 1.
      • Some numbers, like 27, require significantly more steps, illustrating the unpredictable nature of the sequence.
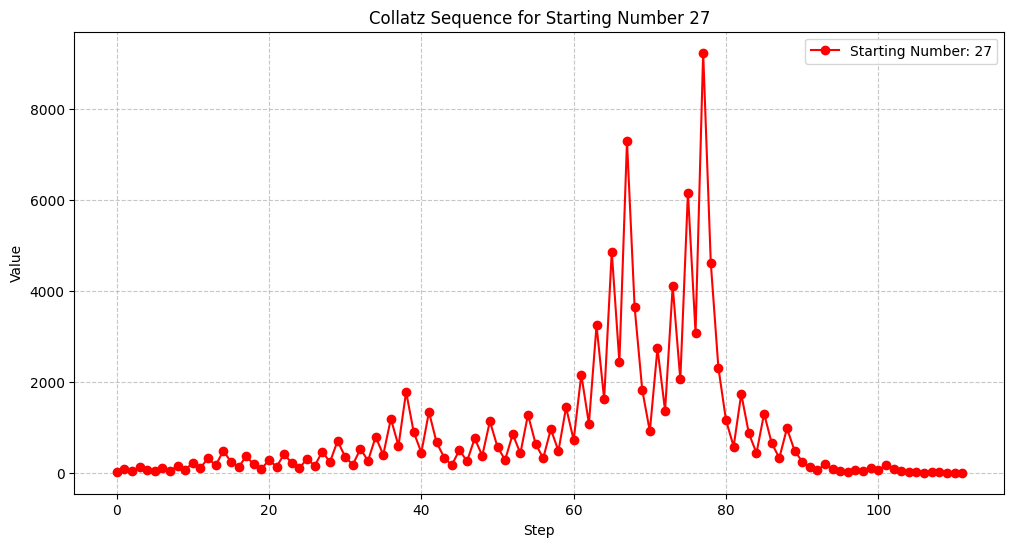
    • Example Sequence:
      • The Collatz sequence for (n=27) is plotted, showing its behavior before eventually reaching 1.

Output

  1. Bar Plot:

    • The number of steps varies widely between starting numbers, demonstrating the complexity of predicting halting behavior.

  2. Sequence Plot:

    • For (n=27), the sequence has a chaotic rise and fall before stabilizing at 1.

This example illustrates the undecidability aspect of the Halting Problem using the unpredictable behavior of the Collatz Conjecture.

While we can compute results for specific inputs, proving general behavior (e.g., all sequences halt) is non-trivial, aligning with the essence of computability theory.