Real-World Problem in Algebra：Polynomial Root Finding in Economics

Problem Statement

A company produces a product whose profit P(x) (in dollars) as a function of production quantity x (in units) is modeled by the polynomial:
P(x)=−2x3+15x2−36x+50

  1. Determine the production quantities x (roots of P(x)=0) where the profit becomes zero (break-even points).
  2. Visualize the profit function P(x) to show its behavior and the identified roots.

Python Implementation

Here’s the Python code to solve the problem and visualize the results:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt
from numpy.polynomial.polynomial import Polynomial

# Define the profit polynomial P(x) = -2x^3 + 15x^2 - 36x + 50
coefficients = [-2, 15, -36, 50]  # Coefficients in decreasing order of powers
poly = np.poly1d(coefficients)

# Find the roots of the polynomial
roots = np.roots(coefficients)

# Generate data for visualization
x = np.linspace(0, 10, 500)  # Production quantity range
y = poly(x)

# Plotting the polynomial
plt.figure(figsize=(10, 6))
plt.plot(x, y, label="$P(x)$ (Profit Function)", color="blue")

# Highlight the roots
real_roots = roots[np.isreal(roots)].real  # Filter real roots
for root in real_roots:
    plt.scatter(root, 0, color="red", zorder=5, label=f"Root at x = {root:.2f}")

# Add annotations and labels
plt.title("Profit Function $P(x)$ and Break-Even Points", fontsize=14)
plt.axhline(0, color="black", linewidth=0.7, linestyle="--", alpha=0.7)
plt.xlabel("Production Quantity $x$", fontsize=12)
plt.ylabel("Profit $P(x)$", fontsize=12)
plt.legend()
plt.grid(alpha=0.3)

# Show plot
plt.show()

# Print results
print("Roots of P(x):", roots)
print("Real roots (Break-even points):", real_roots)

Explanation of Code

  1. Polynomial Representation:

    • The profit function P(x)=−2x3+15x2−36x+50 is represented by its coefficients in decreasing powers of x.
    • The numpy.poly1d function creates a polynomial object for evaluation and visualization.

  2. Root Finding:

    • The roots of P(x) are found using numpy.roots, which computes all roots (real and complex) of the polynomial.
    • Only real roots are relevant in this context as production quantities x must be real numbers.

  3. Visualization:

    • The profit function is plotted over a reasonable range of x values (e.g., x∈[0,10]).
    • Real roots (break-even points) are highlighted on the graph to show where the profit becomes zero.

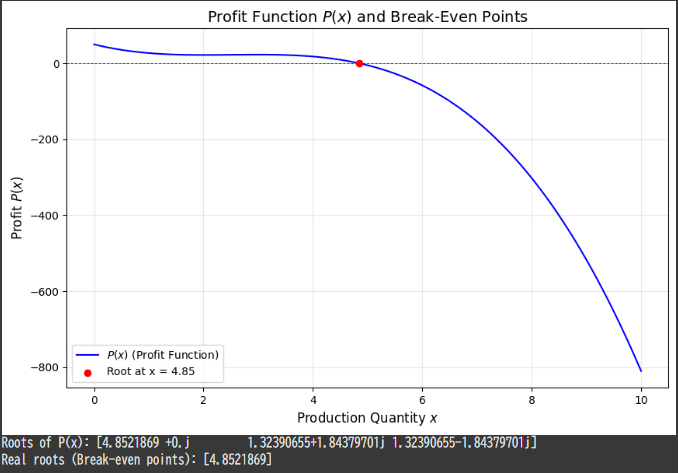
Results and Graph Explanation

  1. Numerical Results:

    • Roots of P(x): These are the solutions to the equation P(x)=0.
      Some may be complex, but only real roots are relevant for this real-world context.
    • Real roots (Break-even points): These are production levels where the company neither makes a profit nor a loss.

  2. Graph:

    • The blue curve represents the profit function P(x).
    • The red points indicate the break-even points where P(x)=0.
    • The curve helps visualize how profit changes with production quantity x, showing regions of profit and loss.

By finding and plotting the roots of the polynomial, the company can identify critical production levels to optimize operations.