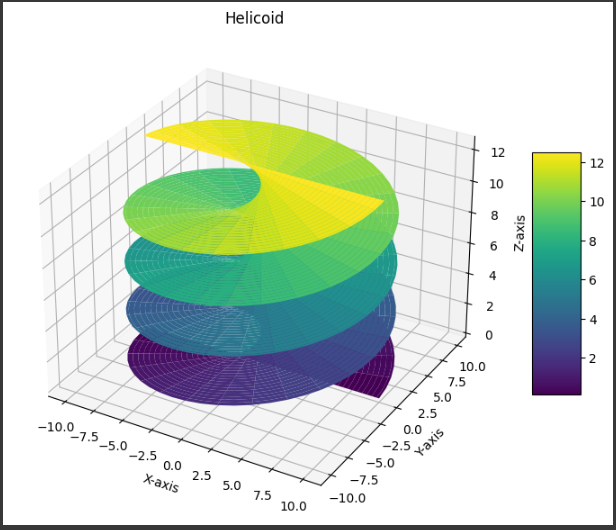
Helicoid（ヘリコイド）

Helicoid（ヘリコイド）

Helicoid（ヘリコイド）を描画してみましょう。

Helicoidは、微分幾何学や応用数学でよく知られている曲面の一つで、螺旋状の形状を持っています。

Helicoidは次のようなパラメトリック方程式で表されます。

$$
x(u, v) = u \cos(v)
$$
$$
y(u, v) = u \sin(v)
$$
$$
z(u, v) = c v
$$

ここで、$( c ) $は螺旋の巻きの間隔を調整する定数です。

プログラム例

以下に、PythonコードでHelicoidを描画する方法を示します。

必要なライブラリのインストール

1
pip install matplotlib numpy

PythonコードでHelicoidを描画

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# パラメトリック方程式のパラメータ範囲を設定
u = np.linspace(-10, 10, 100)
v = np.linspace(0, 4 * np.pi, 100)
u, v = np.meshgrid(u, v)

# Helicoidの定数
c = 1

# Helicoidの方程式
x = u * np.cos(v)
y = u * np.sin(v)
z = c * v

# 3Dプロットを作成
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

# サーフェスプロット
surf = ax.plot_surface(x, y, z, cmap='viridis')

# カラーバー
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

# タイトルと軸のラベルを設定
ax.set_title('Helicoid')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')

# プロットを表示
plt.show()

説明

  1. numpyを使って$u$と$v$の範囲を設定し、グリッドを作成します。
  2. Helicoidのパラメトリック方程式を使用して$x$, $y$, $z$の値を計算します。
  3. matplotlibとmpl_toolkits.mplot3dを使って3Dグラフを描画します。
  4. グラフには軸ラベル、タイトル、カラーバーが含まれています。

このコードを実行すると、螺旋状の形状を持つHelicoidを描画した3Dグラフが表示されます。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. 必要なライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

説明

  • numpy: 数値計算ライブラリであり、配列操作や数学関数の計算に使用します。
  • matplotlib.pyplot: グラフ描画ライブラリであり、データの可視化に使用します。
  • mpl_toolkits.mplot3d.Axes3D: matplotlibの3Dプロット機能を使用するためのモジュールです。

2. パラメトリック方程式のパラメータ範囲を設定

1
2
3
u = np.linspace(-10, 10, 100)
v = np.linspace(0, 4 * np.pi, 100)
u, v = np.meshgrid(u, v)

説明

  • uとvは、Helicoidをパラメトリックに表現するためのパラメータです。
  • np.linspace(start, stop, num)は、startからstopまでの範囲をnum個の等間隔で分割した値を生成します。
    • uは$-10$から$10$までの範囲で$100$個の値を持ちます。
    • vは$0$から$4π$までの範囲で$100$個の値を持ちます。
  • np.meshgrid(u, v)は、uとvのグリッドを作成し、各組み合わせに対して対応するx, y, z座標を計算できるようにします。

3. Helicoidの定数

1
c = 1

説明

  • cはHelicoidの螺旋の巻きの間隔を調整する定数です。
    この例では、cは$1$に設定されています。

4. Helicoidの方程式

1
2
3
x = u * np.cos(v)
y = u * np.sin(v)
z = c * v

説明

  • Helicoidのパラメトリック方程式を用いて、各パラメータに対するx, y, zの値を計算します。
    • x = u * np.cos(v):
      uとvの値を使ってx座標を計算します。
    • y = u * np.sin(v):
      uとvの値を使ってy座標を計算します。
    • z = c * v:
      vの値に定数cを掛けてz座標を計算します。

5. 3Dプロットを作成

1
2
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

説明

  • fig = plt.figure(figsize=(10, 7)):
    図のサイズを指定して新しい図を作成します。
    figsizeは幅と高さをインチ単位で指定します。
  • ax = fig.add_subplot(111, projection='3d'):
    3Dプロット用のサブプロットを追加します。
    • 111は$1$行$1$列のサブプロットグリッドを作成し、その$1$番目のサブプロットを指します。
    • projection='3d'は3Dプロットを作成することを指定します。

6. サーフェスプロット

1
surf = ax.plot_surface(x, y, z, cmap='viridis')

説明

  • ax.plot_surface(x, y, z, cmap='viridis'):
    x, y, zのデータを使って3Dサーフェスプロットを作成します。
    • cmap='viridis'はカラーマップを指定し、サーフェスの色をz軸の値に応じて変化させます。

7. カラーバー

1
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

説明

  • fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5):
    サーフェスプロットのカラーバーを追加します。
    • shrink=0.5はカラーバーの高さを縮小して、全体の高さの$50%$にします。
    • aspect=5はカラーバーのアスペクト比を設定します。

8. タイトルと軸のラベルを設定

1
2
3
4
ax.set_title('Helicoid')
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')

説明

  • ax.set_title('Helicoid'): プロットにタイトル「Helicoid」を設定します。
  • ax.set_xlabel('X-axis'): X軸にラベル「X-axis」を設定します。
  • ax.set_ylabel('Y-axis'): Y軸にラベル「Y-axis」を設定します。
  • ax.set_zlabel('Z-axis'): Z軸にラベル「Z-axis」を設定します。

9. プロットを表示

1
plt.show()

説明

  • plt.show(): 作成した図を表示します。
    このコマンドが実行されると、Helicoidの3Dサーフェスプロットがウィンドウに表示されます。

以上が、コードの各部分の詳しい説明です。

このコードは、Helicoidという螺旋状の形状を持つ曲面を3Dで描画するためのものです。

グラフ解説

[実行結果]

グラフに表示される内容は以下の通りです：

1. グラフの形状

  • Helicoid（ヘリコイド）の形状が描画されます。
    これは螺旋状の形状を持つ曲面であり、中心から外側に向かって広がる形をしています。

2. カラーマップ

  • グラフはカラーマップ（viridis）を使用して色付けされています。
    このカラーマップは高さ（$z$軸の値）に応じて色が変わります。
    これにより、$z$軸方向の変化を視覚的に容易に捉えることができます。

3. カラーバー

  • カラーバーがグラフの右側に表示され、色と高さの対応を示します。
    カラーバーは、サーフェスの高さがどの色に対応するかを示し、$z$軸の値の範囲を視覚化します。

4. タイトルと軸ラベル

  • タイトル: グラフの上部に「Helicoid」というタイトルが表示されます。
    これにより、描画されている曲面がHelicoidであることがわかります。
  • 軸ラベル: 各軸にラベルが付けられています。
    • X軸には「X-axis」
    • Y軸には「Y-axis」
    • Z軸には「Z-axis」

これにより、各軸が何を表しているかが明示されます。

グラフの表示

  • 3Dサーフェスプロットとして、$x$, $y$, $z$の値から計算されたHelicoidの曲面が表示されます。
    曲面は、$u$と$v$という2つのパラメータに基づいて生成される点の集合から形成されています。

これらの要素が組み合わさって、Helicoidの3D曲面が視覚的にわかりやすく表示されています。