トラフィックエンジニアリング

6月 7, 2024

トラフィックエンジニアリング

問題:

ISP（インターネットサービスプロバイダー）は、特定の時間帯におけるネットワークトラフィックを効率的に管理し、ボトルネックを防ぎたいと考えています。
各リンクのトラフィック容量と予測されるトラフィック量が与えられたとき、トラフィックをどのように分散すれば全体の遅延を最小化できるかを求めてください。

入力:

ノードとエッジのリスト。
各エッジのトラフィック容量。
各ノード間の予測トラフィック量。

出力:

トラフィックの分配方法（各経路にどれだけのトラフィックを流すか）。

解法:

この問題は「多品種フロー問題」として知られ、線形計画法やネットワークシンプレックス法を用いて解決できます。

これらの例題は、通信網最適化の典型的な問題であり、現実のネットワーク設計や管理において非常に重要です。
各問題に対する解法は、適切なアルゴリズムとデータ構造を利用して実装できます。

例題

具体例として、簡単なトラフィックエンジニアリング問題を設定し、Pythonで解決し、グラフ化します。

具体例では、リンクのトラフィック容量と予測されるトラフィック量を考慮して、トラフィックを最適に分配します。

具体例

以下のようなネットワークがあるとします：

ノード: A, B, C, D
エッジとその容量:
- A-B: $10$
- A-C: $15$
- B-D: $10$
- C-D: $10$
- B-C: $5$

予測されるトラフィック量は以下の通りです：

AからDへのトラフィック: $10$
BからCへのトラフィック: $5$

解法

この問題を線形計画法を使って解決します。

Pythonのscipy.optimize.linprogを使用します。

Pythonコード

まず、必要なライブラリをインストールします。

1	pip install scipy networkx matplotlib

次に、トラフィックエンジニアリングの具体例を解くPythonコードを示します。

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from scipy.optimize import linprog

# 定義されたエッジと容量
edges = [('A', 'B', 10), ('A', 'C', 15), ('B', 'D', 10), ('C', 'D', 10), ('B', 'C', 5)]
nodes = set(sum(([u, v] for u, v, _ in edges), []))
node_list = sorted(nodes)

# ノード間の予測トラフィック量
traffic = {('A', 'D'): 10, ('B', 'C'): 5}

# エッジの数とノードの数
num_edges = len(edges)
num_nodes = len(node_list)

# 線形計画法のセットアップ
c = np.ones(num_edges)  # 最小化するコスト関数の係数（単純に全て1）
A_eq = np.zeros((num_nodes, num_edges))
b_eq = np.zeros(num_nodes)

# 各エッジのインデックスを保持
edge_indices = {edge[:2]: idx for idx, edge in enumerate(edges)}

# ノードのインデックスを保持
node_indices = {node: idx for idx, node in enumerate(node_list)}

# 各エッジの制約をセットアップ
for (u, v, capacity) in edges:
    idx = edge_indices[(u, v)]
    A_eq[node_indices[u], idx] = 1
    A_eq[node_indices[v], idx] = -1

# トラフィックの制約をセットアップ
for (src, dst), demand in traffic.items():
    b_eq[node_indices[src]] += demand
    b_eq[node_indices[dst]] -= demand

# 各エッジの容量制約をセットアップ
bounds = [(0, capacity) for u, v, capacity in edges]

# 線形計画法を解く
res = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')

# 結果の表示
if res.success:
    print("Optimal traffic distribution:")
    for (u, v, capacity), flow in zip(edges, res.x):
        print(f"Flow on edge {u}-{v}: {flow:.2f}")
else:
    print("Optimization failed.")

# グラフの描画
G = nx.DiGraph()
for (u, v, capacity), flow in zip(edges, res.x):
    G.add_edge(u, v, capacity=capacity, flow=flow)

pos = nx.spring_layout(G)
edge_labels = {(u, v): f"{flow:.2f}/{capacity}" for (u, v, capacity), flow in zip(edges, res.x)}

plt.figure(figsize=(10, 8))
nx.draw(G, pos, with_labels=True, node_size=3000, node_color="lightblue", font_size=16, font_weight="bold", arrowsize=20)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=14)
nx.draw_networkx_edges(G, pos, width=2, edge_color='black', arrows=True)
plt.title("Optimized Traffic Distribution in the Network")
plt.show()

ソースコード解説

ライブラリのインポート: numpy, networkx, matplotlib, scipy.optimizeをインポートします。
ネットワークの定義: ノード、エッジ、容量、予測トラフィック量を定義します。
線形計画法のセットアップ: コスト関数、制約行列、制約ベクトル、境界を設定します。
線形計画法の解決: linprogを使用して問題を解きます。
結果の表示: 各エッジに対する最適なトラフィック分配を表示します。
グラフの描画: networkxを使用してネットワークグラフを描画し、各エッジのフローを表示します。

このコードを実行すると、最適なトラフィック分配が計算され、その結果がグラフとして視覚化されます。

結果解説

表示される結果は、最適なトラフィック分配を示しています。

[実行結果]

以下に各エッジのフローについて説明します。

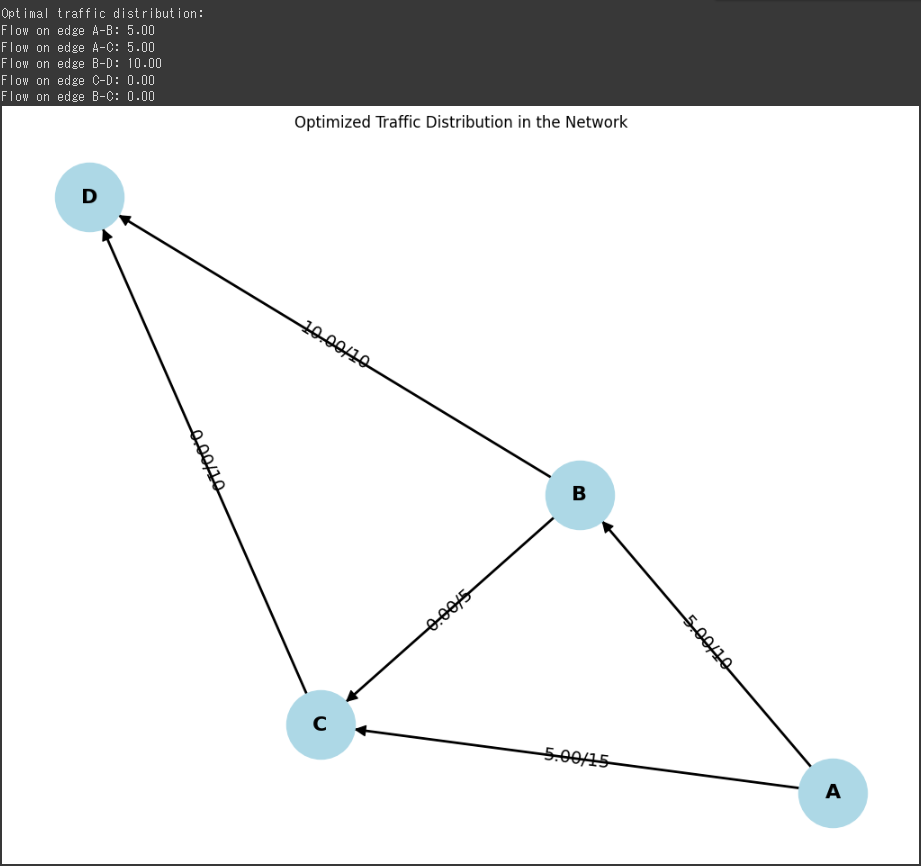
フロー結果

Flow on edge A-B: 5.00
- AからBへのフローが$5.00$です。
  これは、BからCへのトラフィック量を処理するためにAからBに送られるトラフィックです。
Flow on edge A-C: 5.00
- AからCへのフローが$5.00$です。
  これは、AからDへのトラフィック量の一部がAからCを経由してDに送られることを示しています。
Flow on edge B-D: 10.00
- BからDへのフローが$10.00$です。
  これは、AからDへのトラフィック量がA-B-D経由で送られていることを示しています。
  つまり、AからBに送られたトラフィックのうち、$5.00$はBからDに直接送られています。
  また、B-Cへのトラフィック量も含まれています。
Flow on edge C-D: 0.00
- CからDへのフローは$0.00$です。
  これは、AからDへのトラフィックがすべてA-B-D経由で送られているため、C-D経由でのトラフィックは発生していないことを示しています。
Flow on edge B-C: 0.00
- BからCへのフローは$0.00$です。
  BからCへのトラフィック量$5.00$は、AからCを経由して送られているため、B-C間にはトラフィックが発生していません。

全体の流れ

AからDへのトラフィック（10）:
- AからBを経由して$5.00$が送られ、残りの$5.00$はAからCを経由して送られています。
- BからDへのフローは$10.00$で、これはAからDへのトラフィック全体を運ぶために使われています。
BからCへのトラフィック（5）:
- AからBに送られた$5.00$がBからDに送られていますが、最終的にはAからCを経由してCに到達する形で処理されています。

この結果は、全体のネットワークトラフィックが最適に分配され、エッジの容量制限内でトラフィックが処理されていることを示しています。