レムニスケート（Lemniscate）

レムニスケート（Lemniscate）

レムニスケート（Lemniscate）は、双曲線のような形状を持つ数学的な曲線です。

上記のグラフは、レムニスケート・オブ・ベルヌーイ（Lemniscate of Bernoulli）をプロットしたものです。

この曲線は、極座標で表現すると次のようになります：

$$
r^2 = 2 \cos(2\theta)
$$

このグラフの特性をいくつか説明します：

  1. 形状: 曲線は数字の8の字のような形をしています。
    これが「レムニスケート」という名前の由来です。
    レムニスケートはラテン語で「リボン」を意味します。

  2. シンメトリー: 曲線は原点に対して対称であり、$x$軸および$y$軸に対しても対称です。

  3. 定義域: このグラフでは、パラメータ$ ( t ) $を$ (-\pi) $から$ (\pi) $まで変化させて曲線を描いています。

  4. 座標の変換: $x$と$y$の座標は次の式に基づいて計算されます。
    $$
    x = \frac{\sqrt{2} \cos(t)}{1 + \sin^2(t)}
    $$
    $$
    y = \frac{\sqrt{2} \cos(t) \sin(t)}{1 + \sin^2(t)}
    $$

このように、レムニスケートは美しい数学的性質を持ち、解析学や代数幾何学において重要な役割を果たしています。

ソースコード例

以下にレムニスケートをPythonでグラフ化するためのソースコードを示します。

このコードを実行すると、レムニスケート・オブ・ベルヌーイの形状が描かれます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt

# Define the parameter t
t = np.linspace(-np.pi, np.pi, 400)

# Lemniscate of Bernoulli equations
x = np.sqrt(2) * np.cos(t) / (1 + np.sin(t)**2)
y = np.sqrt(2) * np.cos(t) * np.sin(t) / (1 + np.sin(t)**2)

# Plot the Lemniscate
plt.figure(figsize=(8, 8))
plt.plot(x, y)
plt.title("Lemniscate of Bernoulli")
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.grid(color = 'gray', linestyle = '--', linewidth = 0.5)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

このコードについての簡単な説明：

  1. numpy と matplotlib のライブラリをインポートします。
  2. t という変数を$ (-\pi) $から$ (\pi) $までの$400$個の等間隔の点に設定します。
  3. レムニスケート・オブ・ベルヌーイの$ x $座標と$ y $座標を計算します。
  4. plt.plot() 関数を使用して、計算された$ x $と$ y $の値をプロットします。
  5. タイトルや軸ラベル、グリッド線を追加して、プロットを整えます。
  6. plt.show() 関数を使用して、プロットを表示します。

このコードを実行すると、レムニスケートの美しい8の字の形が描かれます。

グラフ解説

[実行結果]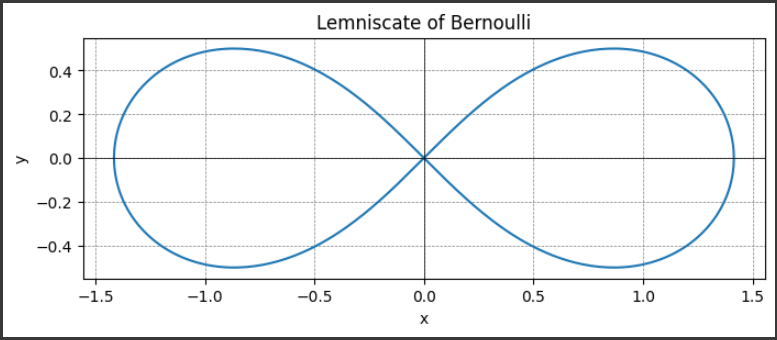

レムニスケート・オブ・ベルヌーイ（Lemniscate of Bernoulli）のグラフについて詳しく説明します。

この曲線は、極座標で次のように表される特定の形状の曲線です：

$$
r^2 = 2 \cos(2\theta)
$$

グラフの内容の説明:

  1. 形状:

    • グラフは数字の「8」の字の形をしています。
      これはレムニスケートの特徴的な形状であり、名前の由来ともなっています（ラテン語で「リボン」を意味します）。

  2. シンメトリー:

    • この曲線は、原点（中心点）に対して対称です。
      また、$x$軸および$y$軸に対しても対称です。
      つまり、グラフの各象限に同じ形状の部分が現れます。

  3. 範囲:

    • $t$パラメータは$(-\pi) $から$ (\pi) $までの範囲を取ります。
      これにより、曲線の全体が描かれます。

  4. 数学的な背景:

    • レムニスケートは、楕円関数や複素解析において重要な役割を果たす数学的な曲線です。
      特に、代数幾何学における研究対象となります。

  5. 座標の計算:

    • 曲線の$ x $座標と$ y $座標は以下の式によって計算されます：
      $$
      x = \frac{\sqrt{2} \cos(t)}{1 + \sin^2(t)}
      $$
      $$
      y = \frac{\sqrt{2} \cos(t) \sin(t)}{1 + \sin^2(t)}
      $$
    • これらの式により、曲線の各点の座標が計算され、プロットされます。

  6. プロットの特徴:

    • グラフは8の字を描き、中心に向かって絞られた形状となります。
    • 縦横の長さが等しいため、グラフは正方形の図形に内接するように表示されます。