マンデルブロ集合

4月 29, 2024

マンデルブロ集合

マンデルブロ集合は、複素数平面上で定義される非常に興味深い集合です。
その定義と性質は以下の通りです。

定義

マンデルブロ集合 Mは、複素平面 C上の点の集合で、以下の漸化式が発散しない点の集まりです。

$$
Z(n+1) = Z(n)^2 + C
$$

ここで、$Z(0) = 0 $で、$C $は複素平面上の任意の点です。

性質

マンデルブロ集合はフラクタル構造を持ち、自己相似性があります。
つまり、任意の拡大率で見ても同じような模様が現れ続けます。
集合は完全に連結しており、ある一点から出発すれば、集合の任意の点に到達できます。
境界上には無数の小さな突起があり、さらにズームインすると、より小さな構造が無限に現れます。
主要な構造体の周りには、無数の小さな副次的構造体があります。
黒い部分は集合に属し、発散しない点を表します。
有色の部分は集合に属さず、その色は発散までの反復回数に応じて変化します。

数学的側面

マンデルブロ集合は、複素数方程式 $ Z(n+1) = Z(n)^2 + C $の解の挙動を視覚化したものです。
この方程式は、カオスや分岐理論などの分野で重要な役割を果たします。
マンデルブロ集合の形状は、方程式の解の安定性や分岐を反映しています。

マンデルブロ集合は美しさと複雑さを併せ持ち、コンピューターによる視覚化によって発見された驚くべき数学的オブジェクトです。

単純な式から生み出されながら、無限の構造を含む不思議な性質を持っています。

ソースコード

Python でマンデルブロ集合をプロットすることができます。

以下のコードでは、numpy と matplotlib を使用しています。

import numpy as np
import matplotlib.pyplot as plt

def mandelbrot(c, max_iter=100):
    z = c
    for n in range(max_iter):
        if abs(z) > 2:
            return n
        z = z*z + c
    return max_iter

width, height = 4, 4
re_start, re_end = -2, 1
im_start, im_end = -1.5, 1.5

re = np.linspace(re_start, re_end, width * 100)
im = np.linspace(im_start, im_end, height * 100)

mandel = np.zeros((height * 100, width * 100))
for i, x in enumerate(re):
    for j, y in enumerate(im):
        mandel[j, i] = mandelbrot(x + 1j * y)

fig, ax = plt.subplots(figsize=(10, 10))
ax.imshow(mandel, cmap='hot', extent=(re_start, re_end, im_start, im_end))
ax.set_title("Mandelbrot Set", fontsize=20)

plt.show()

このコードの解説:

mandelbrot 関数は、複素数 c に対して、マンデルブロ集合の値を計算します。
最大反復回数は max_iter に設定されています。
width、height でプロット領域のアスペクト比を設定し、re_start、re_end、im_start、im_end で複素平面の表示範囲を設定しています。
np.linspace を使って、実数部と虚数部の値の範囲を生成しています。
mandel という空の NumPy 配列を作成し、その要素に mandelbrot 関数の出力値を格納していきます。
plt.imshow で mandel 配列をプロットし、cmap でカラーマップを設定しています。extent で表示範囲を指定しています。

実行すると、以下のようなマンデルブロ集合のプロットが表示されます。

[実行結果]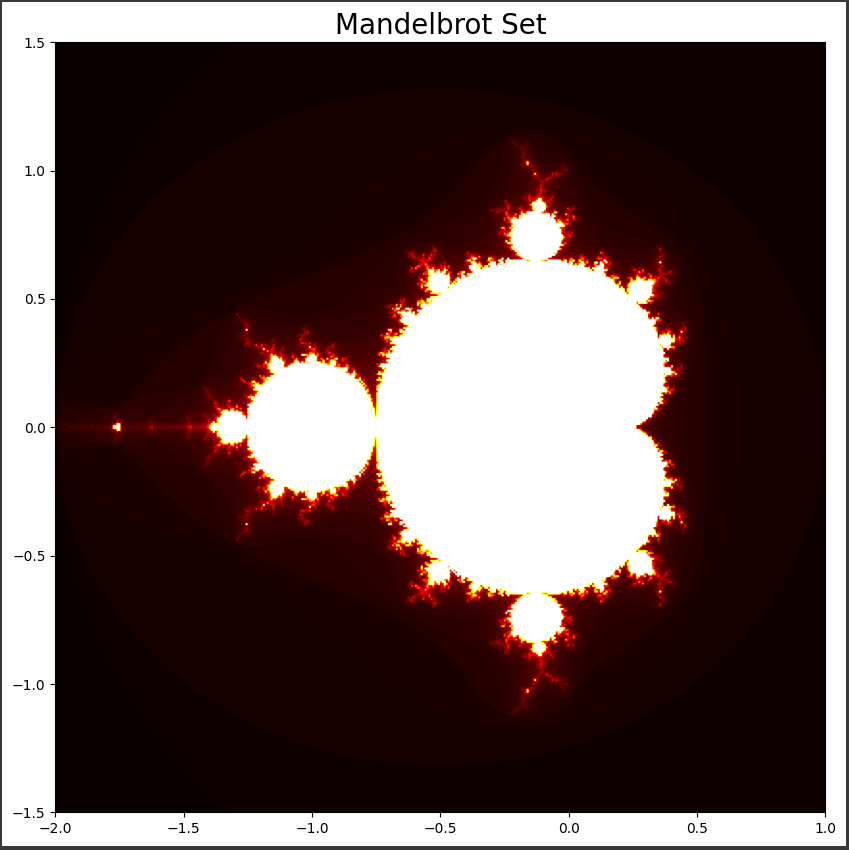

このプログラムでは、繰り返し計算を効率的に行うために NumPy の配列計算を活用しています。

計算量が多いため、大きな解像度で描画するとかなり時間がかかります。

必要に応じて max_iter を調整したり、計算範囲を狭めるなどの最適化が必要です。

また、カラーマップを変更したり、ズームして細部を描画したりと、さまざまな表現が可能です。

ソースコード解説

ソースコードを説明します。

1. ライブラリのインポート

1 2	import numpy as np import matplotlib.pyplot as plt

このコードは、NumPyとmatplotlibライブラリをインポートしています。
NumPyは数値計算に使用され、matplotlibはデータの可視化に使用されます。

2. マンデルブロ集合の計算関数

def mandelbrot(c, max_iter=100):
    z = c
    for n in range(max_iter):
        if abs(z) > 2:
            return n
        z = z*z + c
    return max_iter

この関数は、複素数cに対するマンデルブロ集合の値を計算します。
最大反復回数max_iterを設定し、その回数までに発散しない場合はmax_iterを返します。
発散した場合は、発散するまでの反復回数を返します。

3. グラフ描画領域の設定

1
2
3

width, height = 4, 4
re_start, re_end = -2, 1
im_start, im_end = -1.5, 1.5

ここでは、グラフの描画領域のアスペクト比(width, height)と、複素平面上の表示範囲(re_start, re_end, im_start, im_end)を設定しています。

4. 複素平面上の点の生成

1 2	re = np.linspace(re_start, re_end, width * 100) im = np.linspace(im_start, im_end, height * 100)

np.linspaceを使って、実数部と虚数部の値の範囲を生成しています。
これにより、複素平面上の点を表すグリッドが作成されます。

5. マンデルブロ集合の値の計算と格納

mandel = np.zeros((height * 100, width * 100))
for i, x in enumerate(re):
    for j, y in enumerate(im):
        mandel[j, i] = mandelbrot(x + 1j * y)

まず、mandel配列を$0$で初期化します。
次に、実数部と虚数部の値を組み合わせて複素数を作り、mandelbrot関数を呼び出します。
その結果を、mandel配列の対応する位置に格納します。

6. グラフの描画

fig, ax = plt.subplots(figsize=(10, 10))
ax.imshow(mandel, cmap='hot', extent=(re_start, re_end, im_start, im_end))
ax.set_title("Mandelbrot Set", fontsize=20)
plt.show()

ここでは、matplotlibを使ってマンデルブロ集合をプロットしています。
ax.imshowでmandel配列を画像として表示し、cmap='hot'でカラーマップを設定しています。
extent引数で表示範囲を指定し、ax.set_titleでタイトルを設定しています。
最後にplt.show()でグラフを表示します。

このコードでは、NumPyの効率的な配列計算を活用しながら、マンデルブロ集合の計算と可視化を行っています。
計算量が多いため、大きな解像度で描画するとかなり時間がかかります。

必要に応じてmax_iterを調整したり、計算範囲を狭めるなどの最適化が必要です。

結果解説

[実行結果]

マンデルブロ集合のグラフには、以下のような特徴が表れています。

全体の構造

中心付近に主要な構造体があり、その周りに無数の小さな構造体が存在しています。
主要な構造体は、見た目が肺のような形をしており、複雑で自己相似的なフラクタル構造を持っています。
グラフの外側は黒くなっており、これは発散する点を表しています。

主要な構造体の詳細

主要な構造体の内側は、黒い部分と輝く黄色の部分が入り組んだ複雑な模様になっています。
この構造体の境界線上には、無数の小さな突起や飛び出した部分があり、さらに細かい構造が無限に続いています。
主要な構造体の外側にも、小さな副次的な構造体が多数存在しています。

カラーマップの意味

使用されているカラーマップ (‘hot’)は、青から赤へと徐々に変化する色合いを表しています。
青色の部分は発散するまでの反復回数が少ないことを示し、赤色の部分は反復回数が多いことを示します。
黒い部分は発散しないで無限に計算が続く点を表しています。

自己相似性

マンデルブロ集合の最も印象的な特徴は、自己相似性です。
つまり、構造体の一部を拡大していくと、似たような構造が無限に現れ続けます。
この自己相似性は、フラクタルの典型的な性質です。

マンデルブロ集合は、単純な複素数方程式から生み出された驚くべき構造を持つフラクタルであり、数学的にも美しさがあります。

このグラフは、その複雑で魅力的な構造を視覚化したものです。