ベルヌーイ方程式

ベルヌーイ方程式

ベルヌーイ方程式は、流体力学における基本的な方程式の一つであり、流れの速さと圧力の関係を表現します。

ベルヌーイ方程式は以下の形で表されます：

$$
P + \frac{1}{2} \rho v^2 + \rho gh = \text{constant}
$$

ここで、各項の意味は次の通りです：

  • $(P)$ は流体の圧力
  • $(\rho)$ は流体の密度
  • $(v)$ は流体の速度
  • $(g)$ は重力加速度
  • $(h)$ は流体の高さ

この方程式は、流体のエネルギー保存則を表現しており、特定のポイントでの圧力、速度、高さの変化について関係を示しています。

ベルヌーイ方程式は、流体の流れに関するさまざまな問題で応用されます。

ベルヌーイ方程式をPythonでグラフ化するためには、方程式の関係を適切に表現し、それを可視化する必要があります。

以下に、ベルヌーイ方程式を用いて流体の速度と圧力の関係をグラフ化する例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt

# 定数と流体の特性パラメータ
rho = 1000  # 流体の密度 (kg/m^3)
g = 9.81    # 重力加速度 (m/s^2)
h = 10      # 流体の高さ (m)
constant_term = 100000  # 定数項

# 速度の範囲を定義
v_values = np.linspace(0, 10, 100)  # 0から10までの速度 (m/s)

# 圧力を計算する関数
def calculate_pressure(v):
    return constant_term - 0.5 * rho * v**2 - rho * g * h

# 速度と圧力の関係を計算
pressure_values = calculate_pressure(v_values)

# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(v_values, pressure_values, label='Pressure vs. Velocity')
plt.xlabel('Velocity (m/s)', fontsize=12)
plt.ylabel('Pressure (Pa)', fontsize=12)
plt.title('Bernoulli Equation: Pressure vs. Velocity', fontsize=14)
plt.grid(True)
plt.legend()
plt.show()

このコードでは、与えられた流体の密度 $(\rho)$、重力加速度 $(g)$、流体の高さ $(h)$、および定数項を使用して、ベルヌーイ方程式に基づいて速度と圧力の関係を計算しています。

そして、計算結果をグラフ化しています。

得られるグラフは、速度と圧力の関係を示しており、流体力学におけるベルヌーイ方程式の応用を視覚的に理解するのに役立ちます。

[実行結果]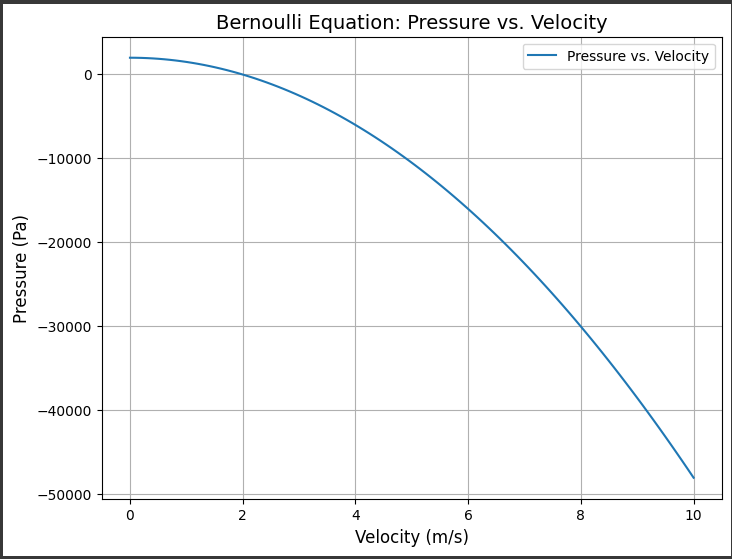

ソースコード解説

ソースコードの詳細な説明を行います。

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpyは数値計算を効率的に行うためのライブラリであり、npとしてインポートされています。
  • matplotlib.pyplotはデータの可視化（グラフ描画）を行うためのライブラリであり、pltとしてインポートされています。

2. 定数と流体の特性パラメータの定義

1
2
3
4
rho = 1000  # 流体の密度 (kg/m^3)
g = 9.81    # 重力加速度 (m/s^2)
h = 10      # 流体の高さ (m)
constant_term = 100000  # 定数項
  • rhoは流体の密度 $（kg/m^3）$を表します。
  • gは重力加速度 $（m/s^2）$を表します。
  • hは流体の高さ $（m）$を表します。
  • constant_termはベルヌーイ方程式の定数項であり、圧力を計算する際に使用されます。

3. 速度の範囲を定義

1
v_values = np.linspace(0, 10, 100)  # 0から10までの速度 (m/s)
  • np.linspace(0, 10, 100)は$0$から$10$までの速度を等間隔で$100$個のデータポイントに区切って生成します。

4. 圧力を計算する関数の定義

1
2
def calculate_pressure(v):
    return constant_term - 0.5 * rho * v**2 - rho * g * h
  • calculate_pressure(v)は、速度 vに対する圧力を計算する関数です。
  • ベルヌーイ方程式に基づいて圧力を計算しています。

5. 速度と圧力の関係を計算

1
pressure_values = calculate_pressure(v_values)
  • v_valuesに対してcalculate_pressure関数を適用して、速度に対する圧力の値を計算します。

6. グラフのプロット

1
2
3
4
5
6
7
8
plt.figure(figsize=(8, 6))
plt.plot(v_values, pressure_values, label='Pressure vs. Velocity')
plt.xlabel('Velocity (m/s)', fontsize=12)
plt.ylabel('Pressure (Pa)', fontsize=12)
plt.title('Bernoulli Equation: Pressure vs. Velocity', fontsize=14)
plt.grid(True)
plt.legend()
plt.show()
  • plt.figure(figsize=(8, 6))で新しい図を作成し、サイズを指定します。
  • plt.plot(v_values, pressure_values, label='Pressure vs. Velocity')で速度と圧力の関係をプロットします。
  • plt.xlabel('Velocity (m/s)', fontsize=12)で$x$軸（横軸）のラベルを設定します。
  • plt.ylabel('Pressure (Pa)', fontsize=12)で$y$軸（縦軸）のラベルを設定します。
  • plt.title('Bernoulli Equation: Pressure vs. Velocity', fontsize=14)でグラフのタイトルを設定します。
  • plt.grid(True)でグリッド線を表示します。
  • plt.legend()で凡例を表示します。
  • plt.show()でグラフを表示します。

このプログラムは、ベルヌーイ方程式に基づいて速度と圧力の関係を計算し、matplotlibを使用してグラフ化しています。

計算された圧力値は、速度が増加するにつれてどのように変化するかを視覚化することができます。

結果解説

[実行結果]

以下は、グラフに表示される内容の詳細な説明です：

1. x軸（横軸）：速度 (Velocity)

  • グラフの横軸は速度 $（m/s）$を表しています。
  • 速度の範囲は$0$から$10$までの値で、$100$個の等間隔なデータポイントがプロットされます。
  • この範囲内で流体の速度がどのように変化するかを示します。

2. y軸（縦軸）：圧力 (Pressure)

  • グラフの縦軸は圧力（$Pa$：パスカル）を表しています。
  • 圧力はベルヌーイ方程式に基づいて計算され、速度の関数としてプロットされます。
  • 速度が変化するとともに、流体の圧力がどのように変動するかを示します。

3. グラフのラベルとタイトル

  • $x$軸（横軸）のラベルは「Velocity ($m/s$)」として設定されています。
    これは流体の速度を表します。
  • $y$軸（縦軸）のラベルは「Pressure ($Pa$)」として設定されています。
    これは流体の圧力を表します。
  • グラフのタイトルは「Bernoulli Equation: Pressure vs. Velocity」として設定されています。
    これはベルヌーイ方程式に基づく圧力と速度の関係を示しています。

4. グリッド線と凡例

  • グラフにはグリッド線が表示されており、視覚的なガイドとして役立ちます。
  • 凡例（Legend）は「Pressure vs. Velocity」として表示され、プロットされたデータの内容を説明しています。

このグラフは、流体の速度が増加すると圧力がどのように変化するかを示しています。

ベルヌーイ方程式は流体力学で重要な法則であり、このグラフを通じて流体の基本的な特性を理解することができます。