パラボロイドの方程式

パラボロイドの方程式

パラボロイドは数学的な曲面であり、放物線を回転させて得られる回転放物面の一種です。
パラボロイドは二次曲面の一種であり、一般的には次のような形式で表されます：

$$
z = \frac{x^2}{a^2} + \frac{y^2}{b^2}
$$

ここで、$( x )$、$( y )$、$( z ) $は空間内の座標を表し、$( a ) $と$ ( b ) $は定数であり、それぞれ$ x軸$方向と$ y軸$方向の放物線の広がりを制御します。

この方程式における放物面は、$( x ) $と$ ( y ) $の値によって$ ( z ) $座標が決まり、放物線の頂点が原点に位置します。
パラボロイドは、放物線が$ x軸$と$ y軸$の両方向に広がっている形状を持ち、$ ( z ) $の値は放物線の広がりに応じて変化します。

Pythonでパラボロイドをグラフ化する際には、このような方程式を用いて$ ( x )$、$( y ) $の範囲を指定し、それに対応する$ ( z ) $の値を計算します。

得られた$ ( x )$、$( y )$、$( z ) $の値を3次元グラフとしてプロットすることで、パラボロイドの形状を視覚化することができます。

ソースコード

以下のPythonコードは、パラボロイドの方程式を解いてグラフ化するものです。

この例では、NumPyとMatplotlibライブラリを使用しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# パラメータ設定
a = 1.0
b = 1.0
c = 1.0

# パラメータの範囲設定
u = np.linspace(-1, 1, 100)
v = np.linspace(-1, 1, 100)
U, V = np.meshgrid(u, v)

# パラボロイドの方程式をパラメータ表示で定義
X = a * U
Y = b * V
Z = c * (U**2 + V**2)

# 3Dプロット
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')

# パラボロイドをプロット
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='k')

# 軸ラベルの設定
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

# グラフのタイトル
plt.title('Paraboloid')

# グラフを表示
plt.show()

このコードでは、a、b、cはパラメータとしてパラボロイドの形状を制御します。

UとVはパラメータの範囲を定義し、X、Y、Zはパラボロイドの方程式に基づいて表面の座標を計算します。

plot_surface関数を使用してパラボロイドを3Dプロットし、軸ラベルやタイトルを設定してグラフを表示します。

[実行結果]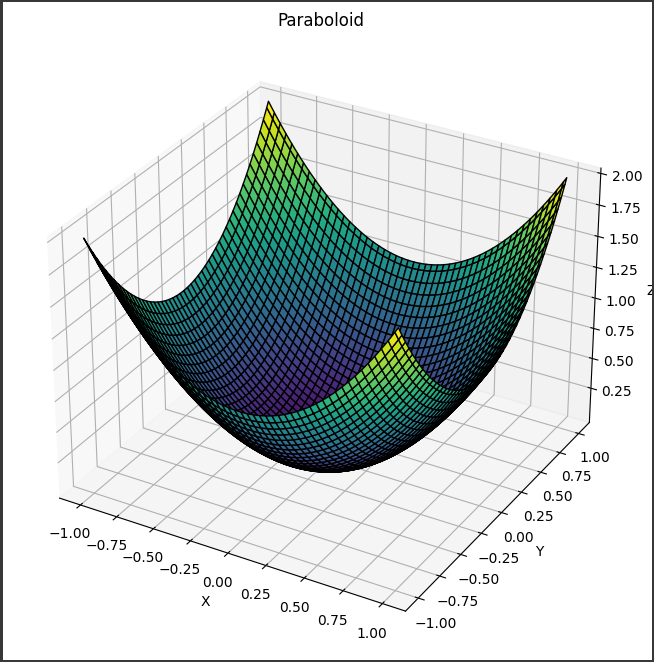

ソースコード解説

このPythonコードは、パラボロイド曲面を生成し、3次元プロットで視覚化するためのものです。

以下にそれぞれの部分を詳しく説明します。

1. ライブラリのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • numpyは数値計算を行うためのライブラリであり、配列や数学関数を効率的に扱います。
  • matplotlib.pyplotはグラフ描画ライブラリで、グラフのプロットやカスタマイズに使用します。
  • Axes3Dは3次元プロット用のクラスを提供します。

2. パラメータ設定:

1
2
3
a = 1.0
b = 1.0
c = 1.0
  • パラボロイドの方程式における定数$ (a)$、$(b)$、$(c) $を設定します。

3. パラメータの範囲設定:

1
2
3
u = np.linspace(-1, 1, 100)
v = np.linspace(-1, 1, 100)
U, V = np.meshgrid(u, v)
  • パラメータ$ (u)$、$(v) $の範囲を設定し、それらの値のメッシュグリッドを作成します。

4. パラボロイドの方程式を定義:

1
2
3
X = a * U
Y = b * V
Z = c * (U**2 + V**2)
  • パラボロイドの方程式$ (z = c(u^2 + v^2)) $をパラメータ$ (U)$、$(V) $を使って定義します。

5. 3Dプロット:

1
2
3
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='k')
  • plot_surfaceメソッドを使用して、パラボロイド曲面を3次元プロットします。
  • cmap='viridis'はカラーマップを設定し、’viridis’は色のマッピングを示します。
  • edgecolor='k'は曲面の枠線の色を黒に設定します。

6. 軸ラベルとタイトルの設定:

1
2
3
4
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.title('Paraboloid')
  • 軸ラベルとグラフのタイトルを設定します。

7. グラフの表示:

1
plt.show()
  • 最後に、プロットされたグラフを表示します。

このコードを実行すると、$(u)$、$(v) $の範囲内で定義されたパラボロイド曲面が3次元空間に表示されます。

結果解説

[実行結果]

上記のPythonコードによって生成されるグラフは、パラボロイド（放物体）の3次元プロットです。

このグラフは以下のような特徴を持っています：

1. 形状:

  • パラボロイドは放物線を回転軸周りに回転させて生成される曲面です。
    この例では、パラメータ a、b、c を調整することでパラボロイドの形状を変えることができます。

2. 色:

  • cmap='viridis' を指定することで、グラフの色をViridisカラーマップに設定しています。
    これにより、高さ（Z軸方向）に応じて色が異なります。
    Viridisは高さが低いときは青色から、高いときは黄色や緑色に変化するカラーマップです。

3. 座標軸:

  • グラフには$X軸$、$Y軸$、$Z軸$があります。
    各軸はそれぞれ X、Y、Z に対応し、パラボロイドの方程式の座標値を示しています。

4. タイトルとラベル:

  • グラフには適切なタイトル ('Paraboloid') が付けられています。
  • $X軸$、$Y軸$、$Z軸$にはそれぞれ 'X'、'Y'、'Z' というラベルが付けられており、各軸の意味を明示しています。

このグラフはパラメータを調整することでパラボロイドの形状を変えることができ、3次元空間で放物体の曲面を視覚化するのに役立ちます。