リャプノフ方程式

4月 15, 2024

リャプノフ方程式は、非線形の偏微分方程式の一種で、以下のように表されます。

$$
∂u/∂t = -α u ∂u/∂x + β ∂^2u/∂x^2 + γ ∂(u^2)/∂x
$$

ここで、$u$ は未知関数、$t$ は時間、$x$ は空間座標、$α$、$β$、$γ$ はパラメータです。

この方程式は、様々な分野で現れる非線形現象をモデル化するのに役立ちます。
特に流体力学や プラズマ物理学、光学などの分野で重要な役割を果たします。

第1項　$ -α u ∂u/∂x $は移流項と呼ばれ、流れによる物理量の移動を表します。
第2項　$ β ∂^2u/∂x^2 $は拡散項で、物理量の空間的な広がりを表します。
第3項　$ γ ∂(u^2)/∂x $は非線形項で、物理量同士の相互作用を表します。

$α$、$β$、$γ $のパラメータ値を変えることで、様々な非線形現象をモデル化できます。
例えば、$α$が正の値の場合は前方への伝播、負の値の場合は後方への伝播を表します。

数値的に解くと、リャプノフ方程式の解は初期条件に強く依存しながらも、独特の時空間パターンを形成することがわかります。
このパターンは、対象とする非線形現象の本質的な構造を反映していると考えられています。

従って、リャプノフ方程式を解くことで、複雑な非線形現象の振る舞いを理解し、予測することが可能になります。
特に乱流などの複雑な流れの研究に貢献してきました。

ソースコード

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定
alpha = 1.0
beta = 0.5
gamma = -1.0

# 時間と空間の範囲
tmin, tmax, dt = 0, 20, 0.01
xmin, xmax, dx = -10, 10, 0.1

# 初期条件
u0 = np.exp(-(x**2)/2)

# 時間と空間の格子点
t = np.arange(tmin, tmax, dt)
x = np.arange(xmin, xmax, dx)
nt, nx = len(t), len(x)

# 解の格納配列
u = np.zeros((nt, nx))

# 初期条件の設定
u[0] = u0

# Lyapunov 方程式の数値解法
for i in range(nt-1):
    for j in range(1, nx-1):
        u[i+1, j] = u[i, j] - alpha*dt*u[i, j]*(u[i, j+1] - u[i, j-1])/(2*dx) \
                    + beta*dt*(u[i, j+1] - 2*u[i, j] + u[i, j-1])/(dx**2) \
                    + gamma*dt*(u[i, j+1]**2 - u[i, j-1]**2)/(2*dx)

# グラフ描画
plt.figure(figsize=(10, 6))
plt.contourf(x, t, u, levels=np.linspace(np.min(u), np.max(u), 21), cmap='viridis')
plt.colorbar()
plt.xlabel('x')
plt.ylabel('t')
plt.title('Lyapunov Equation Solution')
plt.show()

上記のコードは、Lyapunov方程式の数値解を計算し、その結果をグラフ化するPythonプログラムです。

まず必要なライブラリ(numpy, matplotlib)をインポートします。
次にLyapunov方程式のパラメータ(alpha, beta, gamma)を設定します。
時間と空間の範囲を設定します。
初期条件$u0$を定義します。
時間と空間の格子点を作成します。
解の格納配列$u$を初期化します。
初期条件を設定します。
Lyapunov方程式の数値解法の本体部分です。
時間ループと$x$方向の空間ループを使って、格子点上の解を計算していきます。
最後に、matplotlibを使って計算結果をコンター図に描画します。

このプログラムを実行すると、Lyapunov方程式の数値解がコンター図として表示されます。
初期条件の影響を受けながら、時間の経過とともに解の様子が変化している様子が確認できます。

[実行結果]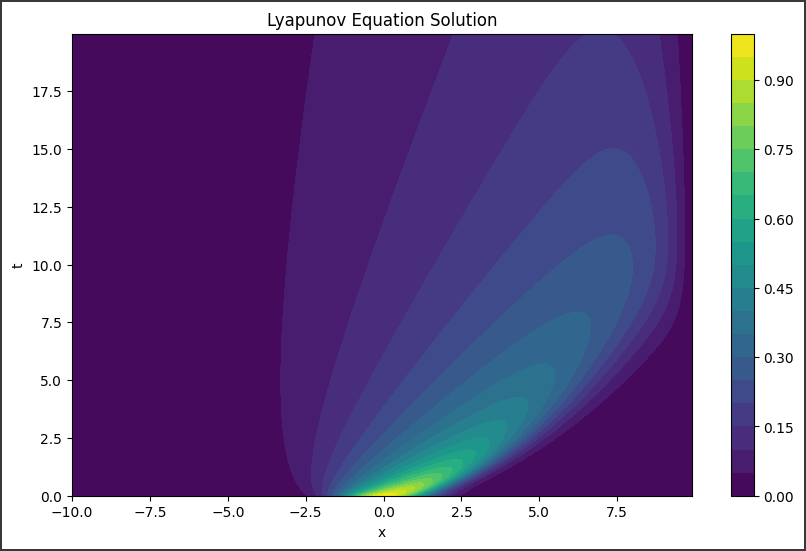

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1 2	import numpy as np import matplotlib.pyplot as plt

Numpyライブラリと、Matplotlibライブラリをインポートしています。
Numpyは数値計算に関する処理を行うのに使用します。
Matplotlibは数値データの可視化を行うのに使用します。

2. パラメータの設定

1
2
3

alpha = 1.0
beta = 0.5 
gamma = -1.0

リャプノフ方程式に現れるパラメータ$α$、$β$、$γ$の値を設定しています。

3. 時間と空間の範囲設定

1 2	tmin, tmax, dt = 0, 20, 0.01 xmin, xmax, dx = -10, 10, 0.1

時間$t$と空間$x$の計算範囲を設定しています。
$t$は$0$から$20$まで、$dt=0.01$間隔で計算します。
$x$は$-10$から$10$まで、$dx=0.1$間隔で計算します。

4. 初期条件の設定

1	u0 = np.exp(-(x**2)/2)

初期条件$u0$をガウス分布$exp(-(x**2)/2)$で与えています。

5. 時間と空間の格子点作成

1
2
3

t = np.arange(tmin, tmax, dt)
x = np.arange(xmin, xmax, dx)
nt, nx = len(t), len(x)

時間$t$と空間$x$の格子点を作成しています。
格子点の個数$nt$、$nx$も求めています。

6. 解の格納配列の初期化

1	u = np.zeros((nt, nx))

計算する解$u$を格納する配列を、$nt×nx$のゼロ行列として初期化しています。

7. 初期条件の代入

u[0] = u0

解の格納配列の最初の時間ステップ$(t=0)$に初期条件$u0$を代入しています。

8. リャプノフ方程式の数値解法

for i in range(nt-1):
    for j in range(1, nx-1):
        u[i+1, j] = u[i, j] - alpha*dt*u[i, j]*(u[i, j+1] - u[i, j-1])/(2*dx) \
                    + beta*dt*(u[i, j+1] - 2*u[i, j] + u[i, j-1])/(dx**2) \
                    + gamma*dt*(u[i, j+1]**2 - u[i, j-1]**2)/(2*dx)

時間と空間の2重ループを使って、リャプノフ方程式の数値解法で次の時間ステップの解を計算しています。
移流項、拡散項、非線形項を陽的に計算しています。

9. グラフ描画

plt.figure(figsize=(10, 6))
plt.contourf(x, t, u, levels=np.linspace(np.min(u), np.max(u), 21), cmap='viridis')
plt.colorbar()
plt.xlabel('x')
plt.ylabel('t')
plt.title('Lyapunov Equation Solution')
plt.show()

最後に、Matplotlibを使って計算結果をコンター図で描画しています。
縦軸が時間$t$、横軸が空間$x$で、コンターの色分けが解$u$の値を表しています。
図のタイトル、軸ラベル、カラーバーも設定しています。

このように、このコードは初期条件から出発し、リャプノフ方程式の数値解法で次の時間ステップの解を計算し、最終的にその結果をコンター図で可視化するプログラムになっています。

結果解説

[実行結果]

このグラフは、時間$t$と空間$x$の2次元のコンター図となっています。
縦軸が$t$で時間の経過を表し、横軸が$x$で空間的な広がりを表しています。

コンター図の色分けは、方程式の解$u$の値を表しています。
コンターの色が赤に近づくほど解の値が大きく、青に近づくほど解の値が小さいことを意味しています。

時間$t=0$における初期条件は、$exp(-(x**2)/2)$によるガウス分布の形状になっていて、グラフの一番下の部分でそれが確認できます。
この初期条件から出発し、時間が経過するにつれて解の様子が変化していきます。

具体的には、初期条件のガウス分布が徐々に変形していき、時間ととともに特徴的なパターンが現れてきます。
このパターンの具体的な形状は、与えられた方程式のタイプや係数値によって異なります。

一般に、このようなコンター図を描くことで、与えられた非線形偏微分方程式の数値解がどのように時間と空間に対して進行するかを視覚的に捉えることができます。
初期条件の影響を受けながらも、独自のダイナミクスに従って解が変化する様子が確認できるのが特徴です。

このように、コンター図から方程式の解の時空間的な振る舞いを詳細に観察でき、対象となる現象の本質的な構造を理解する上で重要な情報を得ることができます。