クラーク-ラムダ分布（Clark-Lambda Distribution）

クラーク-ラムダ分布（Clark-Lambda Distribution）

クラーク-ラムダ分布（Clark-Lambda Distribution）は、確率分布の一種であり、リスク分析や信号処理などの分野で使用されます。

この分布の確率密度関数（PDF）は次のように定義されます:

$$
f(x; \lambda) = \frac{2}{\pi} \frac{\lambda}{\lambda^2 + x^2}
$$

ここで、$(x)$は確率変数であり、$(\lambda)$は分布のパラメータです。

以下は、Pythonでこの分布を解析し、グラフ化する方法の例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt

def clark_lambda_distribution(x, lam):
    return (2 / np.pi) * (lam / (lam**2 + x**2))

# パラメータの設定
lam = 1.0  # λの値

# xの範囲を定義
x_values = np.linspace(-10, 10, 1000)

# 確率密度関数（PDF）を計算
pdf_values = clark_lambda_distribution(x_values, lam)

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

このコードは、$-10$から$10$までの範囲でClark-Lambda分布の確率密度関数を計算し、グラフ化します。

[実行結果]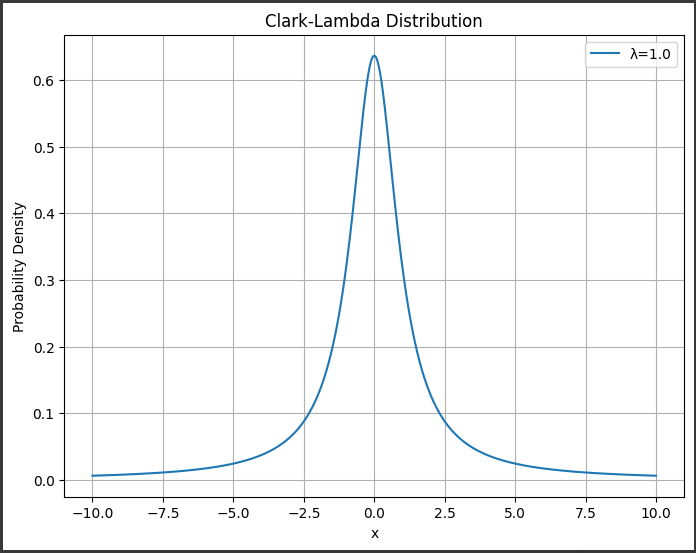

Lambdaパラメータ（λ）を変更することで、異なる分布を観察できます。

ソースコード解説

ソースコードの各部分の説明します。

1. NumPyとMatplotlibのインポート:

1
2
import numpy as np
import matplotlib.pyplot as plt
  • NumPyはPythonで数値計算を行うためのライブラリです。
  • MatplotlibはPythonでグラフ描画を行うためのライブラリです。
    このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. Clark-Lambda分布の確率密度関数を定義する関数:

1
2
def clark_lambda_distribution(x, lam):
   return (2 / np.pi) * (lam / (lam**2 + x**2))
  • clark_lambda_distribution 関数は、Clark-Lambda分布の確率密度関数を計算します。
    引数として x（確率変数）と lam（分布のパラメータ）を受け取ります。

3. パラメータの設定:

1
lam = 1.0  # λの値
  • lam はClark-Lambda分布のパラメータ$ ( \lambda ) $の値を示しています。

4. xの範囲を定義:

1
x_values = np.linspace(-10, 10, 1000)
  • np.linspace 関数を使って、$-10$から$10$の範囲を等間隔で$1000$点に分割した x の値を生成します。
    これにより、確率密度関数のグラフが滑らかになります。

5. 確率密度関数（PDF）を計算:

1
pdf_values = clark_lambda_distribution(x_values, lam)
  • 先ほど定義した clark_lambda_distribution 関数を使って、与えられた x の値とパラメータ$ ( \lambda ) $に基づいてClark-Lambda分布の確率密度関数の値を計算します。

6. グラフをプロット:

1
2
3
4
5
6
7
8
plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
  • Matplotlibを使ってグラフを作成し、Clark-Lambda分布の確率密度関数を表示します。
  • plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
  • plt.plot で x_values と pdf_values をプロットし、ラベルにはパラメータ$ ( \lambda ) $の値が表示されます。
  • plt.title, plt.xlabel, plt.ylabel を使ってタイトルや軸のラベルを設定します。
  • plt.legend() で凡例を表示します。
  • plt.grid(True) でグリッドを有効にし、視覚的な参照を改善します。
  • plt.show() でグラフを表示します。

結果解説

[実行結果]

グラフに表示される内容の詳細な説明です。

1. x軸:

  • x軸は確率変数 $(x)$を表します。
    この確率変数はClark-Lambda分布におけるランダム変数であり、確率密度関数が評価される値の範囲が表示されます。
    ここでは、$-10$から$10$までの範囲が選択されています。

2. y軸:

  • y軸は確率密度関数（PDF）の値を表します。

Clark-Lambda分布の確率密度関数は、$(x)$に関する確率密度を示し、y軸の値はその密度を表します。

3. ラベル:

  • グラフにはClark-Lambda分布の確率密度関数が、指定されたLambdaパラメータ（λ）でプロットされています。
    ラベルにはこのパラメータの値が表示され、グラフ上で異なるパラメータの効果を直感的に理解するのに役立ちます。

4. 凡例:

  • 複数のLambdaパラメータを使用する場合、それぞれの分布が区別できるように凡例が表示されます。
    この例では、唯一のLambdaパラメータが使用されていますが、複数の分布を比較する場合には凡例が重要です。

5. タイトル:

  • グラフのタイトルには、プロットされている分布の種類が示されます。
    この場合、「Clark-Lambda Distribution」と表示されます。

6. グリッド:

  • グラフには背景にグリッドが表示されます。
    これにより、目盛り線に沿ってデータを読み取るのが容易になります。

このグラフは、Clark-Lambda分布の確率密度関数を直感的に理解しやすくするためのものであり、異なるLambdaパラメータを使用することで、分布の形状がどのように変化するかを視覚的に把握できます。