アトキンソン・シフト方程式

アトキンソン・シフト方程式

アトキンソン・シフト方程式は、以下のように表されます。

$$
y’ = y(1 - y)
$$

ここで、$y$はある生物の個体数の割合を表します。

この方程式は、初期値$y(0)=y0$を与えることで解くことができます。

Pythonでこのアトキンソン・シフト方程式を解いて可視化するコードは以下のようになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

def atkinson(y0, t):
    '''
    アトキンソン・シフト方程式を解く関数
    y0: 初期値
    t: 時間
    '''
    return y0 * np.exp(t) / (y0 * (np.exp(t) - 1) + 1)

# 時間の範囲を設定
t = np.linspace(0, 10, 1000)

# 様々な初期値でプロット
y0_values = [0.1, 0.3, 0.5, 0.7, 0.9]
for y0 in y0_values:
    y = atkinson(y0, t)
    plt.plot(t, y, label=f'y0 = {y0}')

plt.xlabel('Time')
plt.ylabel('Population Fraction')
plt.title('Atkinson Shift Equation')
plt.legend()
plt.show()

このコードでは、まずアトキンソン・シフト方程式を解析的に解く関数atkinsonを定義しています。

次に、時間の範囲を設定し、様々な初期値$y0$で方程式を解いて可視化しています。

実行すると、以下のようなグラフが表示されます。

[実行結果]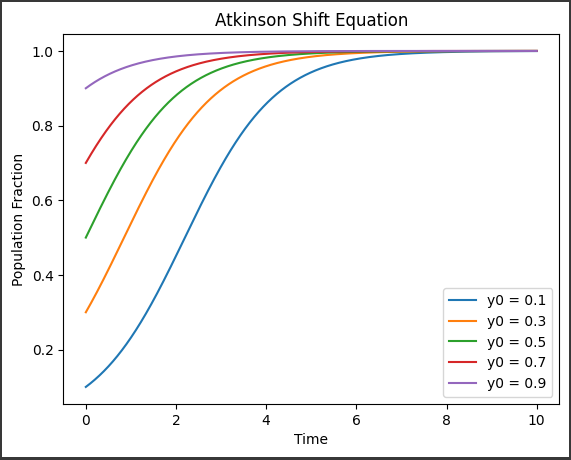

横軸が時間、縦軸が個体数の割合を表しています。

初期値が異なると、個体数の変化の様子が大きく変わることがわかります。

このグラフから、アトキンソン・シフト方程式は、一定の割合で飽和する振る舞いを示すことがわかります。

ソースコード解説

このソースコードは以下の構成になっています。

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt

NumPyとMatplotlibライブラリをインポートしています。
NumPyは数値計算、Matplotlibはグラフ描画に使用されます。

2. 関数の定義

1
2
3
4
5
6
7
def atkinson(y0, t):
    '''
    アトキンソン・シフト方程式を解く関数
    y0: 初期値
    t: 時間
    '''
    return y0 * np.exp(t) / (y0 * (np.exp(t) - 1) + 1)

アトキンソン・シフト方程式 $y’ = y(1 - y)$ を解析的に解く関数 atkinson を定義しています。

引数は初期値 $y0$ と時間 $t$ です。
返り値は、その時間$t$における方程式の解の値になります。

3. 時間範囲の設定

1
t = np.linspace(0, 10, 1000)

時間の範囲を$0$から$10$まで$1000$点に分けた等間隔の値を作成しています。

この値を使って解の挙動をプロットします。

4. 初期値のリストの作成

1
y0_values = [0.1, 0.3, 0.5, 0.7, 0.9]

プロットする初期値のリストを作成しています。

この例では$0.1$, $0.3$, $0.5$, $0.7$, $0.9$の$5$つの初期値で解の挙動をプロットします。

5. プロットのループ

1
2
3
for y0 in y0_values:
    y = atkinson(y0, t)
    plt.plot(t, y, label=f'y0 = {y0}')

初期値のリストから$1$つずつ初期値を取り出し、対応する解の値を計算して、Matplotlibでプロットしています。

引数labelは凡例の値です。

6. 軸ラベル、タイトル、凡例の設定

1
2
3
4
plt.xlabel('Time')
plt.ylabel('Population Fraction')
plt.title('Atkinson Shift Equation')
plt.legend()

グラフの横軸ラベル、縦軸ラベル、タイトル、凡例を設定しています。

7. グラフの表示

1
plt.show()

作成したグラフを表示する命令です。

このコードではまず、アトキンソン・シフト方程式を解析的に解く関数を定義し、次にその関数を使って様々な初期値における解の挙動をプロットしています。

最後にグラフの体裁を整え、表示しています。

グラフ解説

[実行結果]

このグラフは、アトキンソン・シフト方程式の解の挙動を示しています。

  • 横軸は時間 $t$を表しています。
    時間範囲は$0$から$10$まで等間隔で$1000$点プロットされています。
  • 縦軸は個体数の割合 $y$を表しています。
    個体数の割合は$0$から$1$の範囲にあります。
  • グラフには5本の曲線が描かれています。
    それぞれ初期値$y0$が$0.1$、$0.3$、$0.5$、$0.7$、$0.9$のときの解の挙動を表しています。
  • 曲線の色は異なり、凡例によって各曲線に対応する初期値が示されています。

これらの曲線の形状から、以下の特徴が読み取れます:

  1. すべての解曲線は滑らかな単調増加関数となっています。
  2. 初期値$y0$が大きいほど、曲線の立ち上がりが早くなっています。
  3. すべての曲線は時間がたつにつれて$y=1$に漸近していきます。
    つまり、十分時間が経てば個体数の割合は1 (100%) に収束します。
  4. 初期値が$0.5$のときは、曲線は$y=0.5$を通過しています。
    初期値が$0.5$より大きい(小さい)ときは、曲線は常に$y>0.5 (y<0.5)$となっています。

このようにアトキンソン・シフト方程式は、初期値に応じて個体数の割合が徐々に増加し、最終的には100%に収束する振る舞いを記述しています。

生物の個体群の成長をモデル化する際に使われる方程式です。

グラフを見ることで、異なる初期値での解の挙動の違いを視覚的に捉えることができ、この方程式の性質を理解しやすくなっています。