シグモイド関数

シグモイド関数

心理学に関する方程式の例として、心理学的な応答をモデル化するためのシグモイド関数を取り上げます。

シグモイド関数は、入力が増加するにつれて出力が$0$から$1$の間でS字型に変化する関数であり、感情や反応の変化をモデル化するのに適しています。

シグモイド関数は以下のような方程式で表されます：

$$
f(x) = \frac{1}{1 + e^{-x}}
$$

ここで、$ (x) $は入力値です。
この方程式を解き、結果をグラフ化してみましょう。

以下にPythonのコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数の定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# グラフの描画
x_values = np.linspace(-10, 10, 100)
y_values = sigmoid(x_values)
plt.plot(x_values, y_values)
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Sigmoid Function')
plt.grid(True)
plt.show()

このコードは、シグモイド関数をグラフ化します。
入力が増加するにつれて、出力はS字型の曲線で変化することがわかります。

[実行結果]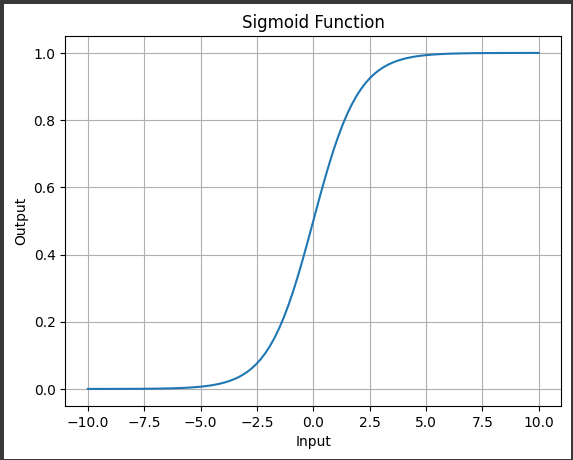

シグモイド関数は、心理学的な応答や感情のモデル化に広く使用されています。

ソースコード解説

このソースコードは、Pythonを使用してシグモイド関数を定義し、その関数をグラフ化するものです。

以下では、コードの詳細な説明を行います。

  1. NumPyとMatplotlibのインポート:

    1
    2
    import numpy as np
    import matplotlib.pyplot as plt

    NumPyは数値計算を行うためのPythonライブラリであり、Matplotlibはグラフ描画ライブラリです。
    これらのライブラリをインポートしています。

  2. シグモイド関数の定義:

    1
    2
    def sigmoid(x):
       return 1 / (1 + np.exp(-x))

    sigmoid 関数は、引数 x に対してシグモイド関数を計算します。
    シグモイド関数は、入力 x に対して以下の式で定義されます：$ [ \frac{1}{1 + e^{-x}} ] $

NumPyの exp 関数を使用して、指数関数の計算を行っています。

  1. グラフの描画:
    1
    2
    3
    x_values = np.linspace(-10, 10, 100)
    y_values = sigmoid(x_values)
    plt.plot(x_values, y_values)
    np.linspace 関数を使用して、$-10$から$10$までの範囲を$100$個の等間隔に区切った x_values を作成します。
    これはグラフの横軸に対応します。

sigmoid 関数を x_values に適用し、対応する y_values を計算します。
これはグラフの縦軸に対応します。

plt.plot 関数を使用して、 x_values と y_values をプロットします。

  1. 軸ラベルとタイトルの追加:

    1
    2
    3
    plt.xlabel('Input')
    plt.ylabel('Output')
    plt.title('Sigmoid Function')

    plt.xlabel 関数と plt.ylabel 関数を使用して、横軸と縦軸のラベルを追加します。
    plt.title 関数を使用して、グラフのタイトルを追加します。

  2. グリッドの表示:

    1
    plt.grid(True)

    plt.grid 関数を使用して、グリッドを表示します。
    これにより、グラフ内のデータの配置がより見やすくなります。

  3. グラフの表示:

    1
    plt.show()
  • plt.show 関数を使用して、作成したグラフを表示します。

このコードは、シグモイド関数の特性を示すグラフを作成するものです。

結果解説

[実行結果]

上記のコードによって生成されたグラフは、シグモイド関数の特性を示しています。

1. 横軸（X軸）:

横軸は入力値を表しています。
ここでは、$-10$から$10$までの範囲を$100$個の等間隔で区切っています。

2. 縦軸（Y軸）:

縦軸はシグモイド関数の出力を表しています。
出力は$0$から$1$の間の値をとります。
入力が増加するにつれて、出力が$0$に近づきます（入力が大きくなると$0$に近づく）。

3. グラフの形状:

グラフはS字型の曲線を描いており、これがシグモイド関数の特徴です。
この曲線は入力が増加するにつれて徐々に上昇し、最終的には$1$に収束します。
この曲線は非線形であり、入力値の変化に応じて出力が急速に変化します。

4. 特性:

シグモイド関数は、入力値の変化に応じて$0$から$1$までの範囲で滑らかに変化するため、感情や心理的反応のモデリングに適しています。
例えば、刺激の増加に対する感情の変化や、行動の確率を予測する際に使用されます。

このグラフは、シグモイド関数の理解を支援し、心理学や機械学習などの分野での応用に役立ちます。