ケプラーの法則

ケプラーの法則

惑星に関する方程式の例として、惑星の軌道を記述するケプラーの法則を取り上げます。
第一法則によれば、惑星の軌道は楕円軌道であり、その楕円の中心には太陽が位置しています。

ケプラーの第一法則の方程式は楕円の方程式で表されます:

r(θ)=a(1−e2)1+e⋅cos(θ)

ここで、(r)は太陽からの距離、(θ)は中心からの角度、(a)は長半径、(e)は離心率です。

これをPythonで実装してグラフ化しましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt

# ケプラーの法則に基づく関数
def kepler(theta, a, e):
    r = a * (1 - e**2) / (1 + e * np.cos(theta))
    return r

# 角度の範囲を設定
theta = np.linspace(0, 2 * np.pi, 1000)

# 惑星の軌道のパラメータ
a = 1.0  # 長半径
e = 0.5  # 離心率

# 楕円軌道を計算
r = kepler(theta, a, e)

# 楕円をプロット
plt.figure(figsize=(8, 6))
plt.plot(r * np.cos(theta), r * np.sin(theta), label='Orbit')
plt.scatter(0, 0, color='yellow', label='Sun')  # 太陽の位置をプロット
plt.gca().set_aspect('equal', adjustable='box')
plt.title('Kepler\'s First Law')
plt.xlabel('Distance (AU)')
plt.ylabel('Distance (AU)')
plt.legend()
plt.grid(True)
plt.show()

このコードは、指定された長半径と離心率に基づいて楕円軌道を計算し、それをプロットしています。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してケプラーの法則に基づいた楕円軌道を計算し、グラフ化するものです。

以下に各部分の詳細を示します。

1. ライブラリのインポート:

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpyは数値計算を行うためのライブラリで、配列や数学関数などを提供します。
  • matplotlib.pyplotはグラフ描画のためのライブラリで、グラフの作成やカスタマイズができます。

2. ケプラーの法則に基づく関数の定義:

1
2
3
def kepler(theta, a, e):
   r = a * (1 - e**2) / (1 + e * np.cos(theta))
   return r
  • kepler関数は、与えられた角度(θ)、長半径(a)、離心率(e)に基づいて惑星の楕円軌道の距離(r)を計算します。

3. 角度の範囲の設定:

1
theta = np.linspace(0, 2 * np.pi, 1000)
  • np.linspace関数を使用して、0から(2π)までの範囲を等間隔で1000点に分割した角度の配列を生成します。

4. 惑星の軌道のパラメータの設定:

1
2
a = 1.0  # 長半径
e = 0.5  # 離心率
  • 楕円軌道の長半径(a)と離心率(e)を設定します。

5. 楕円軌道の計算:

1
r = kepler(theta, a, e)
  • kepler関数を使用して、与えられた角度、長半径、離心率に基づいて楕円軌道の距離を計算します。

6. 楕円のプロット:

1
2
3
4
5
6
7
8
9
10
plt.figure(figsize=(8, 6))
plt.plot(r * np.cos(theta), r * np.sin(theta), label='Orbit')
plt.scatter(0, 0, color='yellow', label='Sun')  # 太陽の位置をプロット
plt.gca().set_aspect('equal', adjustable='box')
plt.title('Kepler\'s First Law')
plt.xlabel('Distance (AU)')
plt.ylabel('Distance (AU)')
plt.legend()
plt.grid(True)
plt.show()
  • plt.figure()で新しい図を作成し、figsizeで図のサイズを設定します。
  • plt.plot()で楕円軌道をプロットします。
  • plt.scatter()で太陽の位置をプロットします。
  • plt.gca().set_aspect('equal', adjustable='box')で軸のアスペクト比を等しく設定します。
  • plt.title()、plt.xlabel()、plt.ylabel()でタイトルと軸ラベルを設定します。
  • plt.legend()で凡例を表示します。
  • plt.grid(True)でグリッドを表示します。
  • plt.show()でグラフを表示します。

これにより、ケプラーの法則に基づいた惑星の楕円軌道がプロットされます。

結果解説

[実行結果]

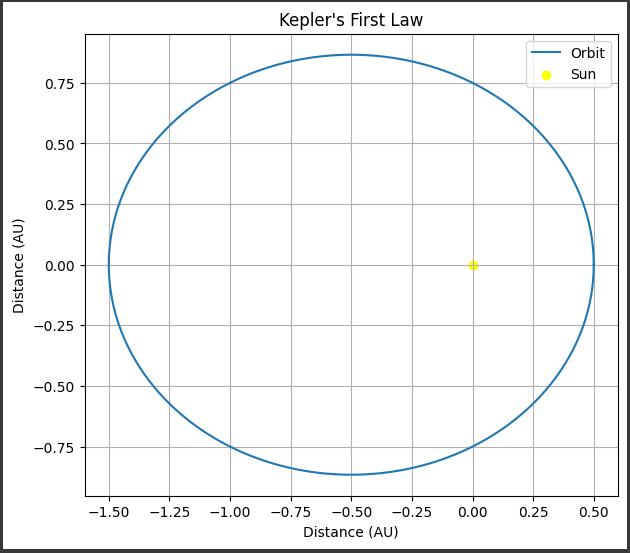
このグラフは、ケプラーの第一法則に基づいて計算された惑星の楕円軌道を示しています。

楕円軌道:

グラフ上の曲線は、惑星が太陽の周りを周回する軌道を表しています。
この軌道は楕円であり、太陽を焦点とする楕円です。
楕円の中心には太陽があります。

太陽:

グラフ上で黄色い点が描かれています。
これは太陽を表しています。
楕円の中心に太陽があることを示しています。

軌道の形状:

楕円の形状は、長半径(a)と離心率(e)の値によって決まります。
長半径が大きいほど楕円はより円に近くなり、離心率が0に近いほど楕円は円に近づきます。
離心率が1に近いほど楕円はより細長くなります。

軌道の対称性:

楕円は太陽を中心に対称的です。
これは、惑星が太陽の周りを一定の軌道速度で一定の軌道周期で回ることを意味します。

座標軸:

x軸とy軸はそれぞれ惑星の軌道上の点のx座標とy座標を表しています。
この座標系は楕円軌道の形状を正しく表現しています。

このグラフは、惑星が楕円軌道を描くことを直感的に理解しやすくするために使用されます。