複雑な数式

複雑な数式

次のような多項式関数を考えてみましょう。

$$
f(x) = x^4 - 6x^3 + 11x^2 - 6x
$$

この多項式関数を Python で解析し、グラフ化することができます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import matplotlib.pyplot as plt

# 多項式関数の定義
def f(x):
    return x**4 - 6*x**3 + 11*x**2 - 6*x

# xの値を生成
x_values = np.linspace(-1, 4, 400)  # グラフ化する範囲を指定

# 対応するyの値を計算
y_values = f(x_values)

# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, y_values, label='f(x) = x^4 - 6x^3 + 11x^2 - 6x', color='blue')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Graph of a Complex Polynomial Function')
plt.legend()
plt.grid(True)
plt.show()

このコードは、$ ( f(x) = x^4 - 6x^3 + 11x^2 - 6x ) $の関数を生成し、範囲$ ([-1, 4]) $の$x値$に対応する$y値$を計算してグラフ化します。

[実行結果]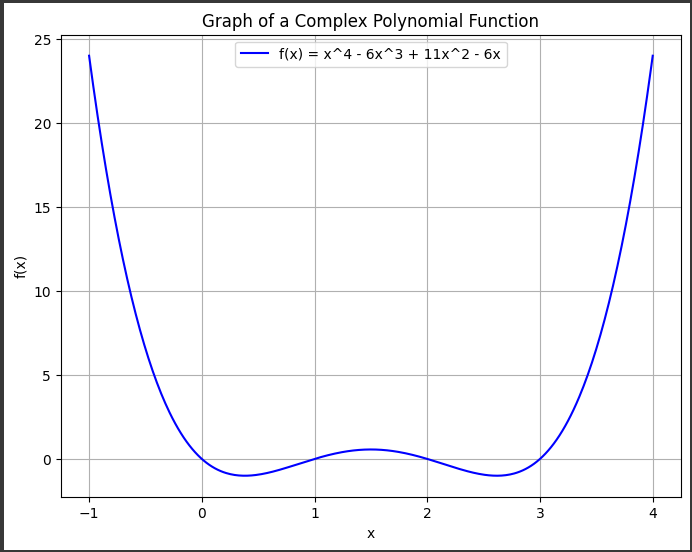

このようにして、複雑な数式の挙動を視覚化することができます。

ソースコード解説

このソースコードは、Pythonを使用して複雑な多項式関数のグラフを描画するものです。

以下に、コードの章立てと詳細な説明を示します。

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • numpyは数値計算を行うためのライブラリで、特に配列や行列の操作が得意です。
  • matplotlib.pyplotはグラフの描画をサポートするライブラリです。

2. 多項式関数の定義

1
2
def f(x):
    return x**4 - 6*x**3 + 11*x**2 - 6*x
  • f(x)は4次の多項式関数を表しています。

3. xの値の生成

1
x_values = np.linspace(-1, 4, 400)
  • -1から4までの範囲を等間隔に区切り、400点のxの値を生成しています。

4. 対応するyの値の計算

1
y_values = f(x_values)
  • 生成したxの値に対応するyの値を関数f(x)を用いて計算しています。

5. グラフのプロット

1
2
3
4
5
6
7
8
plt.figure(figsize=(8, 6))
plt.plot(x_values, y_values, label='f(x) = x^4 - 6x^3 + 11x^2 - 6x', color='blue')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Graph of a Complex Polynomial Function')
plt.legend()
plt.grid(True)
plt.show()
  • plt.figure(figsize=(8, 6))で図のサイズを指定しています。
  • plt.plot(x_values, y_values, label='f(x) = x^4 - 6x^3 + 11x^2 - 6x', color='blue')でグラフをプロットしています。ラベルと色も指定しています。
  • plt.xlabel('x')とplt.ylabel('f(x)')でx軸とy軸のラベルを指定しています。
  • plt.title('Graph of a Complex Polynomial Function')でグラフのタイトルを指定しています。
  • plt.legend()で凡例を表示します。
  • plt.grid(True)でグリッドを表示します。
  • plt.show()でグラフを表示します。

このコードは、指定された多項式関数をグラフに描画し、その形状や特徴を可視化しています。

結果解説

[実行結果]

上記のコードにより描画されるグラフは、4次の多項式関数$ f(x) = x^4 - 6x^3 + 11x^2 - 6x $の形状を示しています。

以下に、グラフの詳細な説明を行います。

1. 関数の形状:

グラフは典型的な4次関数の形状を示しています。
関数の次数が高いため、複雑な曲線が描かれています。

2. xとyの範囲:

$x軸$は$ -1 $から$ 4 $までの範囲で、$y軸$は関数$ f(x) $の値に対応しています。
この範囲で関数がどのように振る舞っているかが確認できます。

3. 関数のゼロ点:

グラフがx軸と交わる点が関数のゼロ点です。
これらの点は、関数の解や根を表しています。

4. 極小点と極大点:

グラフ上の極小点や極大点は、関数の極小値や極大値に対応しています。
これらの点は曲線の谷や山を示しています。

5. 凡例:

グラフには凡例が表示されており、「f(x) = x^4 - 6x^3 + 11x^2 - 6x」というラベルが付いています。
これは描画されている曲線がどの関数に対応しているかを示しています。

6. タイトル:

グラフの上部には「Graph of a Complex Polynomial Function」というタイトルがあり、描画されている関数が複雑な多項式関数であることを示しています。

7. グリッド:

グラフにはグリッドが表示されており、目盛りが曲線上の位置を正確に読み取るのに役立ちます。

このグラフは、数学的な関数の視覚的な表現として使用され、関数の特徴や挙動を理解するのに役立ちます。