ポートフォリオ最適化問題

ポートフォリオ最適化問題

ポートフォリオ最適化問題の例を、3つの資産（ビットコイン、イーサリアム、米ドル）で考え、3Dグラフ化します。

以下のPythonコードでは、それぞれの資産への投資比率を調整し、ポートフォリオのリターンを最大化するように最適化します。

各投資比率は$0$から$1$の間の値をとり、全体の和は$1$となる制約があります。

必要となるライブラリをインストールします。

1
!pip install cvxpy matplotlib numpy

それでは、3Dでのグラフ化を含む以下のコードをご覧ください。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# ビットコイン、イーサリアム、米ドルのリターン
r_btc = 7.0
r_eth = 5.0
r_usd = 2.0

# 投資比率の変数 (0 ≦ x, y ≦ 1)
x = cp.Variable() # ビットコインへの投資比率
y = cp.Variable() # イーサリアムへの投資比率

# 目的関数 - ポートフォリオリターンの最大化
objective = cp.Maximize(r_btc * x + r_eth * y + r_usd * (1 - x - y))

# 制約条件
constraints = [x >= 0, y >= 0, x + y <= 1]

# 最適化問題の定義
prob = cp.Problem(objective, constraints)

# 3Dグラフ描画のための範囲とグリッドを作成
btc_range = np.linspace(0, 1, 100)
eth_range = np.linspace(0, 1, 100)
b, e = np.meshgrid(btc_range, eth_range)
usd_range = 1 - b - e

# 最適化問題を解く
result = prob.solve()

print("最大ポートフォリオリターン: ", result)
print("最適なビットコインへの投資比率: ", x.value)
print("最適なイーサリアムへの投資比率: ", y.value)
print("最適な米ドルへの投資比率: ", 1 - x.value - y.value)

# 3Dプロットの作成
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# ポートフォリオのリターンをZ軸としてプロット
Z = r_btc * b + r_eth * e + r_usd * usd_range
mask = np.where(usd_range < 0, np.nan, Z)

ax.plot_surface(b, e, mask, rstride=1, cstride=1, color='b', alpha=0.2, zorder=-1)

# 最大化問題の点をプロット
ax.scatter(x.value, y.value, result, color="r", s=100)

ax.set_xlabel('Bitcoin')
ax.set_ylabel('Ethereum')
ax.set_zlabel('Return')

plt.show()

ちなみになりますが、多資産のポートフォリオ最適化は非常に複雑であり、多くの場合、相関関係、リスク等の他の要因を考慮する必要があります。

上記のコードは理論上の模範であり、実際の投資判断には利用しないでください。

[実行結果]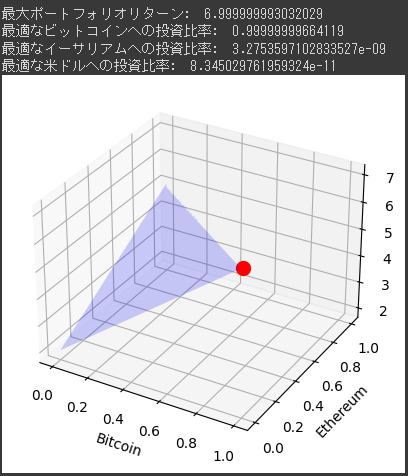

ソースコード解説

このPythonスクリプトは、cvxpyを使用して投資ポートフォリオの最適化問題を解き、3Dグラフを作成しています。

1. モジュールのインポート:

cvxpy、numpy、matplotlibの必要なモジュールをインポートしています。
cvxpyは最適化問題を解くためのライブラリです。

2. リターンの設定:

ビットコイン、イーサリアム、米ドルのリターンをそれぞれ変数r_btc、r_eth、r_usdに設定しています。

3. 変数の定義:

投資比率を示す変数x（ビットコインへの投資比率）とy（イーサリアムへの投資比率）をcvxpyの変数として定義しています。

4. 目的関数と制約条件の定義:

最大化したいポートフォリオリターンを目的関数として定義し、投資比率が$0$以上で、合計が$1$以下であるという制約条件を設定しています。

5. 最適化問題の定義と解決:

cvxpyを使用して最適化問題を定義し、.solve()メソッドを使って問題を解いています。

6. 最適化結果の出力:

解をresultに格納し、最適な投資比率を表示しています。

7. 3Dプロットの作成:

ビットコインとイーサリアムへの投資比率をX軸とY軸に、ポートフォリオのリターンをZ軸にした3Dグラフを作成しています。
赤い点は最大化されたポートフォリオの点を示しています。

このコードは、ビットコインとイーサリアムの投資比率を最適化し、ポートフォリオのリターンを視覚化しています。

結果解説

[実行結果]

この3Dグラフは、ビットコイン、イーサリアム、米ドルという3つの異なる資産に対する投資比率（X軸はビットコイン、Y軸はイーサリアム）と、それらの投資比率から導かれるポートフォリオのリターン（Z軸）の関係を示しています。

頂上の赤い点は、投資比率を最適化することによって達成可能な最大ポートフォリオリターンを示しています。

これは、ビットコイン、イーサリアム、米ドルへの最適な投資比率を用いた場合のリターンです。

このグラフを見ると、一部の領域が存在しないことに気づくかもしれません。

これは、ビットコイン、イーサリアム、米ドルへの投資比率の合計が100%を超えることはできないためです。

これら3つの資産への投資合計が1（または100%）を超える投資比率の組み合わせは不可能であり、そのためグラフから除外されています。

この3Dグラフはあくまで理論的なもので、実際の市場環境や投資戦略、リスク許容度によって最適なポートフォリオは変動します。

だからと言って、このグラフが無意味であるわけではありません。

次元の異なる複数の資産を持つポートフォリオのリターンを視覚化する一助となり、リスクとリターンのトレードオフを理解する上で有用なツールです。