最適化問題（3Dグラフ） CVXPY

最適化問題（3Dグラフ）

以下は、Pythonで3Dグラフを用いて最適化問題を解いて可視化する例です。

この例では、CVXPYを使用して、変数 $x$, $y$ の2つを持つ最適化問題を解きます。

目的関数は$ x^2 + y^2 $で、制約条件は$ x + y <= 1 $です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 変数の定義
x = cp.Variable()
y = cp.Variable()

# 目的関数の定義
objective = cp.Minimize(x**2 + y**2)

# 制約条件の定義
constraints = [x + y <= 1]

# 最適化問題の定義
prob = cp.Problem(objective, constraints)

# 最適化問題の解決
result = prob.solve()

# 解を出力
print("Optimal value:", result)
print("Optimal x:", x.value)
print("Optimal y:", y.value)

# 3Dプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

x_vals = np.linspace(-1, 1, 100)
y_vals = np.linspace(-1, 1, 100)
x_mesh, y_mesh = np.meshgrid(x_vals, y_vals)
z = x_mesh**2 + y_mesh**2

ax.plot_surface(x_mesh, y_mesh, z, cmap='viridis', alpha=0.8)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Objective function')

# 最適解をプロット
opt_x = x.value
opt_y = y.value
opt_z = opt_x**2 + opt_y**2
ax.scatter(opt_x, opt_y, opt_z, color='red', s=100, label='Optimal point')

plt.title('Optimization with CVXPY and 3D Plotting')
plt.legend()
plt.show()

このコードでは、$x$と$y$の値を変化させた際の2変数関数$ x^2 + y^2 $を3Dプロットし、最適化された点を赤い点で示しています。

[実行結果]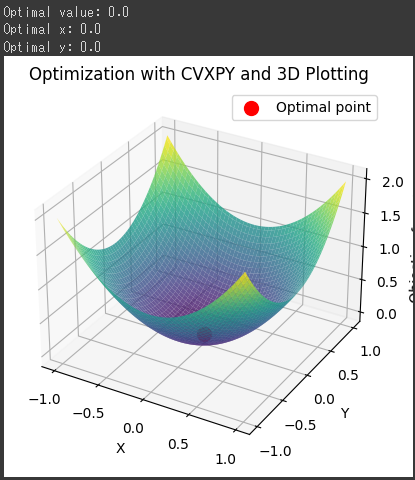

ソースコード解説

このコードは、CVXPYを使用して最適化問題を解き、その結果を3Dプロットで可視化するものです。

以下はソースコードの詳細な説明です。

ライブラリのインポート

  • cvxpy as cp: CVXPYをcpとしてインポートします。
  • numpy as np: NumPyをnpとしてインポートします。
  • matplotlib.pyplot as plt: Matplotlibのpyplotモジュールをpltとしてインポートします。
  • mpl_toolkits.mplot3d: Matplotlibの3Dプロットを利用するためのモジュールです。

変数の定義

  • xとyはCVXPYの変数として定義されます。
    これらの変数は最適化問題の変数として使用されます。

目的関数の定義

  • objectiveは、最小化する目的関数を表しています。
    ここでは、$ (x^2 + y^2) $を最小化するように設定されています。

制約条件の定義

  • constraintsは、制約条件のリストです。
    この場合、$ (x + y \leq 1) $という制約条件が定義されています。

最適化問題の定義

  • probは、最適化問題を表します。
    objectiveとconstraintsを引数として渡して最適化問題を定義します。

最適化問題の解決

  • prob.solve()は、定義した最適化問題を解きます。
    最適な変数の値を見つけ、最小値を求めます。

解の出力

  • 求めた最適な変数の値と最適値を表示します。

3Dプロット

  • plt.figure(): 新しい図を作成します。
  • fig.add_subplot(111, projection='3d'): 3Dのサブプロットを追加します。
  • x_valsとy_valsは、それぞれ$-1$から$1$までの$100個$の等間隔の値を持つ配列です。
    これを使ってメッシュグリッドを生成します。
  • x_meshとy_meshはx_valsとy_valsを使って作成された格子状のデータです。
    それらに基づいて目的関数の値zを計算します。
  • ax.plot_surface(): メッシュグリッドを使用して3Dの曲面をプロットします。
    cmapはカラーマップ、alphaは透明度を指定します。
  • ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel(): 各軸のラベルを設定します。

最適解のプロット

  • ax.scatter(): 最適解を赤い点でプロットします。
    これは、最適解の$ (x) $と$ (y) $の値に対応する目的関数の値を表します。

グラフの表示

  • plt.title(): グラフのタイトルを設定します。
  • plt.legend(): 凡例を追加します。
  • plt.show(): グラフを表示します。

結果解説

[実行結果]

このコードは、CVXPYを使用して2変数の最適化問題を解き、その結果を3Dグラフで可視化しています。

最適化問題は、目的関数 $ (x^2 + y^2) $を最小化するというもので、制約条件は$ (x + y \leq 1) $です。
これは、2変数$ (x) $と$ (y) $の値を持つ平面上で$ (x^2 + y^2) $を最小化する問題です。

プログラムでは、変数$ (x) $と$ (y) $を定義し、目的関数および制約条件を設定しました。
その後、CVXPYを使って最適化問題を解決し、最適解の$ (x) $と$ (y) $の値を得ています。

3Dグラフでは、平面上の$ (x) $と$ (y) $の値を範囲指定してメッシュグリッドを生成し、それに対応する$ (x^2 + y^2) $の値を計算してプロットしています。
これにより、2変数関数$ (x^2 + y^2) $の3D表面が描かれます。

最適解は、求めた$ (x) $と$ (y) $の値を赤い点で表現しています。
これは、目的関数を最小化する最適な $ (x) $と$ (y) $の値を示しています。

つまり、このグラフは、2変数関数を3Dで可視化し、最適解を視覚的に示しています。