関数をグラフ化

関数をグラフ化

次の関数をグラフ化します。

$$
[
f(x) = \frac{\sin(x)}{x}
]
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt

# 関数を定義
def f(x):
    return np.sin(x) / x

# xの範囲を設定
x = np.linspace(-10, 10, 1000)
x = x[x != 0]  # ゼロを除外（分母がゼロになるのを防ぐため）

# 関数をグラフにプロット
plt.figure(figsize=(8, 6))
plt.plot(x, f(x), label='$\\frac{\\sin(x)}{x}$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Graph of $f(x) = \\frac{\\sin(x)}{x}$')
plt.legend()
plt.grid(True)
plt.show()

これにより、 $ (f(x) = \frac{\sin(x)}{x}) $のグラフが表示されます。

[実行結果]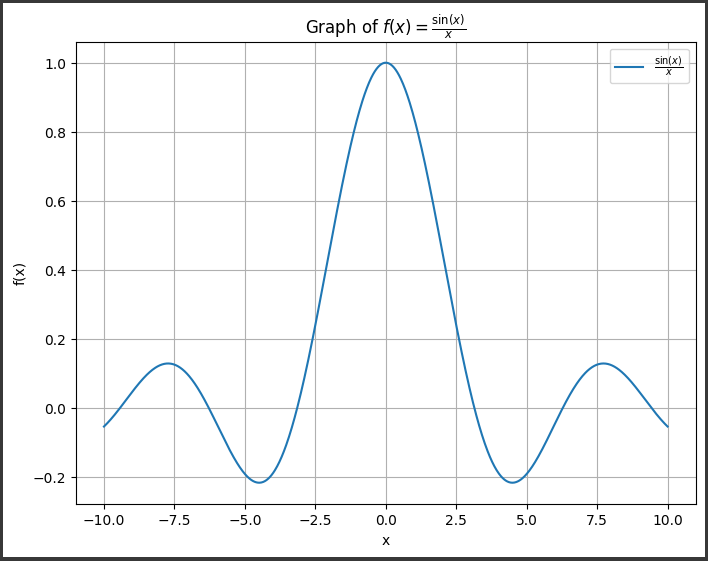

ソースコード解説

このコードは、関数$ (f(x) = \frac{\sin(x)}{x}) $を定義し、それをグラフ化しています。

  1. numpy ライブラリを使って、連続的な$ (x) $の範囲を設定しています。
    linspace 関数は、-10から10までの間を等間隔に分割し、1000点の$ (x) $座標を生成しています。

  2. ただし、分母がゼロになる$ (x=0) $の点を除外するために、x から$ (x=0) $の点を取り除いています。

  3. f(x) の値を計算し、関数の値を取得します。

  4. matplotlib を使ってグラフを描画します。
    生成した$ (x) $座標とそれに対応する関数の値をプロットしています。

  5. グラフの軸ラベル、タイトル、凡例、グリッド線などが設定されています。

このコードを実行すると、関数$ (f(x) = \frac{\sin(x)}{x}) $のグラフが生成され、その特性が視覚化されます。

特に、$ (x) $がゼロに近いところでの挙動や、$ (x) $が大きくなるにつれて関数がゼロに収束する様子などが観察できます。

グラフ解説

[実行結果]

このグラフは関数 $ (f(x) = \frac{\sin(x)}{x}) $を表しています。
この関数は、$ (x) $の値がゼロに近づくにつれて、分母がゼロになりますが、 $ (\sin(x)) $は$ (x) $がゼロの近くでもゼロにならないため、関数は$ (x=0) $で定義されます。

グラフは、$ (x) $がゼロに近いところで$ (\frac{\sin(x)}{x}) $の値が大きく振動し、$ (x) $の絶対値が大きくなるにつれて、関数の値がゼロに近づく様子を示しています。

関数は$ (x=0) $で未定義ですが、その周辺で連続に振る舞い、$ (x) $が大きくなると関数の値はゼロに収束していきます。

グラフ全体が周期的な特徴を持ち、$ (x) $がゼロに近いところで特に振動が大きくなっています。