3次元ガウス関数

3次元ガウス関数は、多変量ガウス分布を表現するための関数です。

以下は3次元ガウス関数の式です。

$$
[ f(x, y) = \frac{1}{2\pi\sigma_x\sigma_y}e^{-\frac{1}{2}\left(\frac{(x-\mu_x)^2}{\sigma_x^2} + \frac{(y-\mu_y)^2}{\sigma_y^2}\right)} ]
$$

ここで、$ (x) $と$ (y) $は変数で、$ (\mu_x) $と$ (\mu_y) $はそれぞれ$ (x) $と$ (y) $の平均、$ (\sigma_x) $と$ (\sigma_y) $は標準偏差です。

Pythonで3次元ガウス関数をグラフ化するための例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

def gaussian_2d(x, y, mux, muy, sigmax, sigmay):
    return (1. / (2 * np.pi * sigmax * sigmay) * 
            np.exp(-0.5 * ((x - mux)**2 / sigmax**2 + (y - muy)**2 / sigmay**2)))

# ガウス関数のパラメータ設定
mux = 0
muy = 0
sigmax = 1
sigmay = 1

x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = gaussian_2d(x, y, mux, muy, sigmax, sigmay)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('3D Gaussian Function')

plt.show()

このコードでは、2つの変数$ (x) $と$ (y) $のガウス関数を計算し、3次元プロットを作成しています。

平均と標準偏差の値を変更すると、関数の形状がどのように変わるかを観察できます。

[実行結果]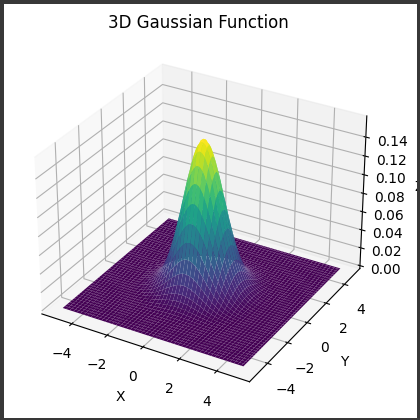

ソースコード解説

このコードは、2変数の2次元ガウス関数を作成し、その関数を3次元プロットで視覚化するためのものです。

以下、詳細な説明です：

1. import文:

  • matplotlib.pyplotからpltをインポートしています。
    これはグラフの描画に使用されます。
  • numpyからnpをインポートしています。
    これは数値計算に使用されます。
  • mpl_toolkits.mplot3dからAxes3Dをインポートしています。
    これは3次元プロットのための機能を提供します。

2. gaussian_2d関数:

  • 2変数の2次元ガウス関数を定義しています。
    この関数は、座標 (x, y) に対するガウス関数の値を返します。

3. ガウス関数のパラメータ設定:

  • mux、muy、sigmax、sigmay は、ガウス関数の平均と標準偏差を設定するためのパラメータです。

4. np.linspace()を使って x と y の値を生成:

  • np.linspace()は指定された範囲内で一定間隔の値を生成します。

5. np.meshgrid()を使って x と y の格子を作成:

  • np.meshgrid()は x と y の2つの1次元配列を受け取り、それぞれの組み合わせに対する格子を作成します。

6. gaussian_2d()関数を使って x と y に対するガウス関数の値 z を計算:

  • gaussian_2d()関数は、先ほど定義したガウス関数を使用して、各 (x, y) 座標でのガウス関数の値を計算します。

7. plt.figure()を使って図を作成:

  • plt.figure()は新しい図を作成します。

8. fig.add_subplot()を使って3Dサブプロットを追加:

  • fig.add_subplot()は図に新しい3次元のサブプロットを追加します。

9. ax.plot_surface()を使って3Dプロットを作成:

  • ax.plot_surface()は x、y、z 座標上のデータから3次元プロットを作成します。
    cmap='viridis'はカラーマップを設定します。

10. ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel()を使って軸ラベルを設定:

  • それぞれ X、Y、Z 軸のラベルを設定します。

11. ax.set_title()を使ってグラフタイトルを設定:

  • グラフにタイトルを追加します。

12. plt.show()でグラフを表示:

  • plt.show()は作成したグラフを表示します。

このコードは、2変数の2次元ガウス関数を計算し、それを3次元プロットとして視覚化しています。